 We only consider here the relations at object class level;
We only consider here the relations at object class level; We left out the n-ary relationship.
We left out the n-ary relationship.


We made two assumptions:
 We only consider here the relations at object class level;
We only consider here the relations at object class level; We left out the n-ary relationship.
We left out the n-ary relationship.
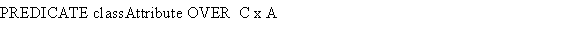
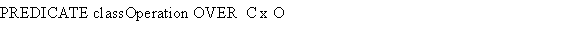

Every object can have several instantiations.
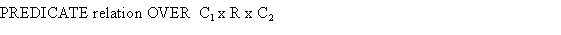




A relation can be an association, an aggregation or an inheritance. With this knowledge we can form the association, aggregation and inheritance classes.

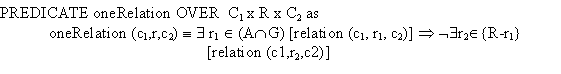
There can exist several associations between two classes. But when there exists an aggregation or an inheritance relation, there can not be another relation
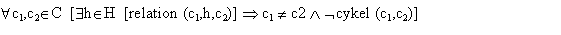
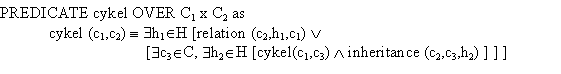
There exist some extra rules for an inheritance relation. It is not possible for a subclass, to be a super class for his own super class (directly or indirectly). This is stated in the above definitions.
In the first predicate we state that you can not inherit from your own class, and that there can not exist a cycle of inheritances between a superclass and a subclass.
This cycle is defined as follows: when A is the superclass of B, then B is the superclass of A, or there exists a class C, which is a subclass of B and a superclass (directly or indirectly) of A. With this recursive definition, you will always find a cycle when there is one present.
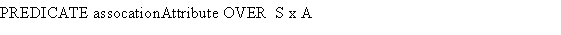
An association can have a so called 'link attribute'.
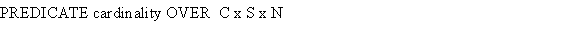
Every association is assigned a number for each side of the association, called the multiplicity or cardinality. This number denotes how many instances of a class, can be linked to an instance of the other class.
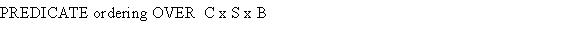
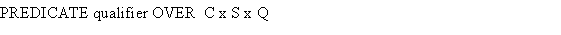
An association can be ordered at one side, or qualified.

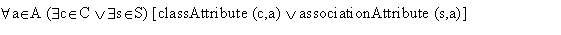

 You can not have an aggregate where the aggregate object is the same as the element object
You can not have an aggregate where the aggregate object is the same as the element object We have not explicitly stated anything about multiple inheritance, but we have not ruled it out either!
We have not explicitly stated anything about multiple inheritance, but we have not ruled it out either!

 Last modified: February 8th, 1996
Last modified: February 8th, 1996