Università di Foggia
Dipartimento di Scienze Biomediche
Prof. Crescenzio Gallo

c.gallo@unifg.it
L'ambiente di calcolo scientifico Mathematica
Una breve panoramica
Front-end
Il front end è il modulo che consente di lavorare con Mathematica sfruttandone non solo le potenzialità di calcolo ma anche le molteplici funzionalità di editor di testi scientifici e di visualizzazione dei dati, ad esempio per mezzo di grafici in due e tre dimensioni. Esso dispone di numerose funzioni e comandi, richiamati tramite la barra dei menù. I fogli di lavoro vengono chiamati notebook e possono essere utilizzati sia per scrivere testi scientifici o semplici commenti, sia per eseguire calcoli e visualizzare grafici.
Da un punto di vista generale, si può semplificare il ruolo del front end, affermando che questo modulo si preoccupa di dialogare con l’utente, attraverso l’acquisizione delle sue richieste e la rappresentazione delle informazioni in una maniera ad egli comprensibile.
La palette contiene una serie di bottoni utili per inserire, in un testo o in una linea di input, i simboli speciali più diffusi nella letteratura scientifica. L’utilizzo delle palette risulta molto comodo quando si usa Mathematica per i calcoli immediati, ossia per inserire richieste di computazioni direttamente dal front end. Infatti, è spesso utile scrivere le espressioni utilizzando la sintassi classica, quella che ricorre ai simboli quali ad esempio la radice quadrata ![]() , l’integrale ∫, la sommatoria ∑, la produttoria ∏ o le lettere dell’alfabeto greco.
, l’integrale ∫, la sommatoria ∑, la produttoria ∏ o le lettere dell’alfabeto greco.
Ad esempio, per calcolare la radice quadrata di un numero utilizzando la forma più immediata per il sistema (definita anche InputForm) si potrebbe scrivere Sqrt[n], ma il front end permette di utilizzare il simbolo![]() . Allo stesso modo, se si vuole calcolare la somma di n numeri indicizzati del tipo
. Allo stesso modo, se si vuole calcolare la somma di n numeri indicizzati del tipo ![]() si può utilizzare il simbolo di sommatoria
si può utilizzare il simbolo di sommatoria 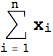 al posto della funzione
al posto della funzione ![]() .
.
Le espressioni che contengono simboli, quali ad esempio ![]() e
e ![]() , vengono anche chiamate espressioni bidimensionali.
, vengono anche chiamate espressioni bidimensionali.
Il Kernel
Il kernel ha un compito molto più arduo dal punto di vista dell’efficienza e della computazione, dovendo effettuare tutti i calcoli necessari per arrivare alla risposta sulla base delle richieste inserite dall’utente.
Una volta che il front end ha appurato che la richiesta può essere inoltrata, traduce l’espressione scritta dall’utente in qualcosa di comprensibile al kernel e glielo invia; a questo punto il kernel esegue le operazioni necessarie attivando gli algoritmi corrispondenti e, una volta portati a termine i calcoli, restituisce la risposta al front end, il quale riconverte le informazioni in un formato comprensibile all’utente mostrandole in video.
Da un punto di vista generale, si può dire che il kernel è un’ampia e ricca libreria di algoritmi per la risoluzione di calcoli numerici, simbolici e grafici, che può essere ulteriormente ampliata dall’utente semplicemente programmando nuove routine con il linguaggio stesso di Mathematica.
La sintassi e le regole di base
Il notebook è un foglio di lavoro interattivo nel quale, se si desidera ricevere una risposta dal sistema, la domanda formulata deve rispettare una serie di regole.
La prima lettera di una parola-chiave del sistema viene sempre scritta in maiuscolo. Nel caso di funzioni con nomi composti, entrambi i nomi devono essere scritti con la prima lettera maiuscola e, per funzioni il cui nome è composto da una sola lettera, questa sarà ovviamente maiuscola.
La regola appena descritta lascia intuire che Mathematica ha un interprete case sensitive, ossia effettua una distinzione tra lettera minuscola e maiuscola.
In virtù del fatto che i notebook possono essere anche utilizzati come documenti di testo, il tasto ![]() (Invio) viene interpretato dal front end come un carriage return (carattere di a capo); per questo motivo quando, invece, si intende far valutare il contenuto di una cella bisogna premere contemporaneamente i tasti
(Invio) viene interpretato dal front end come un carriage return (carattere di a capo); per questo motivo quando, invece, si intende far valutare il contenuto di una cella bisogna premere contemporaneamente i tasti ![]() (shift + invio) oppure il tasto Enter (se presente), per indicare al front end che l’intero contenuto della cella deve essere mandato al kernel per l’interpretazione dei comandi in esso inclusi.
(shift + invio) oppure il tasto Enter (se presente), per indicare al front end che l’intero contenuto della cella deve essere mandato al kernel per l’interpretazione dei comandi in esso inclusi.
Avendo introdotto i concetti e le nozioni fondamentali per cominciare ad utilizzare Mathematica, si prosegue ora con alcuni esempi di calcolo, che serviranno anche ad introdurre ulteriori principi utili ad approfondire la conoscenza del sistema.
Alcuni esempi di calcolo
Si supponga di voler calcolare le radici di una equazione di secondo grado del tipo ![]() . La funzione che ci interessa è la Solve. Quando si chiede al sistema una certa computazione, bisogna indicare almeno due cose: l’operazione da effettuare (Solve nell’esempio) e l’argomento su cui effettuarla (l’equazione
. La funzione che ci interessa è la Solve. Quando si chiede al sistema una certa computazione, bisogna indicare almeno due cose: l’operazione da effettuare (Solve nell’esempio) e l’argomento su cui effettuarla (l’equazione ![]() nell’esempio). Il passaggio degli argomenti avviene mediante la coppia di parentesi quadre [] che ne delimitano l’inizio e la fine. Una volta completata la scrittura della richiesta, basta premere i tasti
nell’esempio). Il passaggio degli argomenti avviene mediante la coppia di parentesi quadre [] che ne delimitano l’inizio e la fine. Una volta completata la scrittura della richiesta, basta premere i tasti ![]() contemporaneamente. Si avrà così:
contemporaneamente. Si avrà così:
![]()
![]()
La prima cosa che si nota è che la cella di input viene aggiornata con una etichetta (label) del tipo In[1]:=, mentre la cella successiva, contenente la risposta generata dal kernel, presenta una etichetta del tipo Out[1]:=. Questo sta ad indicare che tutte le operazioni che vengono effettuate durante una sessione di lavoro vengono etichettate e memorizzate dal sistema in ordine cronologico. Tale ordine torna utile nel momento in cui si vuole recuperare l’output di una computazione già eseguita in precedenza, senza dover ripetere le operazioni che hanno generato tale output; infatti mediante l’uso della combinazione di simboli %n si può ottenere nuovamente l’output numero n, senza che venga rielaborato il corrispondente input. Se, in un qualunque momento della sessione di lavoro, si vogliono riutilizzare le radici dell’equazione mostrate nella cella etichettata In[1]:=, basta scrivere:
![]()
![]()
Ritornando alla scrittura dell’equazione ![]() , per ottenere l’elevamento a potenza si può utilizzare sia l’espressione x^2 (chiamata InputForm, la forma standard per l’inserimento degli input con solo testo standard), sia l’espressione bidimensionale
, per ottenere l’elevamento a potenza si può utilizzare sia l’espressione x^2 (chiamata InputForm, la forma standard per l’inserimento degli input con solo testo standard), sia l’espressione bidimensionale ![]() , ottenibile tramite la palette Basic Math Input. Inoltre, per rappresentare un’equazione, bisogna utilizzare la notazione del doppio uguale (==) tra il primo ed il secondo membro.
, ottenibile tramite la palette Basic Math Input. Inoltre, per rappresentare un’equazione, bisogna utilizzare la notazione del doppio uguale (==) tra il primo ed il secondo membro.
Si riportano ora altre informazioni utili per l’inserimento di simboli ed espressioni bidimensionali direttamente dalla tastiera, evitando l’utilizzo delle palette. Ad esempio, l’espressione seguente:
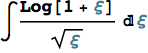
![]()
si può scrivere utilizzando la sequenza di tasti di seguito riportata, dove sono sottolineate le sequenze di tasti che corrispondono a simboli speciali. Si noti che le sequenze del tipo ![]() indicano che i tasti vanno digitati l’uno dopo l’altro, mentre quelle del tipo
indicano che i tasti vanno digitati l’uno dopo l’altro, mentre quelle del tipo ![]() indicano che i tasti vanno premuti contemporaneamente nella sequenza specificata:
indicano che i tasti vanno premuti contemporaneamente nella sequenza specificata:
![]() Log[1+
Log[1+ ![]() ]
] ![]()
![]()
![]()
![]()
![]()
![]()
Ancora un’altra espressione bidimensionale:
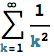
![]()
ottenibile tramite la sequenza:
![]()
![]() k=1
k=1 ![]()
![]()
![]() 1
1 ![]() k
k ![]() 2
2 ![]()
Per inserire le espressioni bidimensionali direttamente da tastiera, in genere, è indispensabile ricorrere all’utilizzo dei tasti di controllo quali ![]() e
e ![]() . Per l’inserimento dei simboli, invece, oltre alla possibilità di utilizzare i tasti di controllo, ad esempio
. Per l’inserimento dei simboli, invece, oltre alla possibilità di utilizzare i tasti di controllo, ad esempio ![]() , vi è la possibilità di utilizzare la seguente sintassi:
, vi è la possibilità di utilizzare la seguente sintassi:
\[NomeSimbolo]
Appena terminata di scrivere la parentesi di chiusura nella forma sopra riportata, il front end provvede a sostituire quanto scritto con il corrispondente simbolo. Si provi a completare con la parentesi quadra chiusa ] le seguenti espressioni:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
La tabella che segue riporta la sintassi da utilizzare per l’inserimento da tastiera di alcuni simboli.
Sequenza
Simbolo
\[EscapeKey]
[ESC]
\[RightTriangle]
|>
\[Placeholder]
□
\[SelectionPlaceholder]
■
\[Infinity]
∞
\[Implies]
⇒
\[Epsilon]
ε
\[Element]
∈
\[ForAll]
∀
\[Exists]
∃
\[And]
∧
\[Or]
∨
\[CirclePlus]
⊕
\[CircleTimes]
⊗
Infine, si ricorda che le lettere dell’alfabeto greco si ottengono anche tramite la sequenza di ![]()
Sequenza
Simbolo
[ESC] a [ESC]
α
[ESC] b [ESC]
β
[ESC] c [ESC]
χ
…
…
[ESC] y [ESC]
ψ
Un’altra regola di sintassi da ricordare è l’utilizzo delle parentesi. Mathematica interpreta le parentesi in maniera differente rispetto alla tradizionale notazione scientifica. Infatti, ad esempio, per indicare una funzione di una variabile bisognerà scrivere f[x] e non f(x). La tabella che segue riepiloga il significato attribuito da Mathematica alle varie forme di parentesi:
Forma
Significato
Esempio
( )
Raggruppamento nelle espressioni algebriche
x (y+z) → x y + x z
[ ]
Passaggio di argomenti
![]()
{ }
Delimitazione delle liste
{{1,2,3},{4,5,6},{6,7,8}}
[[ ]]
Parte di un oggetto (ad esempio lista)
{a,b,c}[[2]] → b
(* *)
Delimitazione dei commenti nelle righe di input
var = 2+3 (* var salva il risultato *)
Dunque, scrivere f(2) significa moltiplicare la funzione f per 2, mentre f[2] significa valutare la funzione f nel punto 2.
L’Help in linea
Mathematica offre tre differenti livelli di help, differenziati per il tipo di informazioni fornite. Vi sono due diversi help in linea, ottenibili direttamente dal notebook di lavoro. Se si vuole sapere semplicemente il comportamento di una funzione e quali argomenti utilizzare si può chiedere un help di primo livello utilizzando il simbolo ?
![]()
Se invece si vogliono sapere ulteriori informazioni sulla funzione si può chiedere un help più descrittivo utilizzando il simbolo ??, che fornisce, oltre al messaggio precedente, anche qualche indicazione aggiuntiva sulle caratteristiche della funzione:
![]()
| Attributes[Solve]={Protected} | |
|
I comandi ? e ?? permettono anche l'uso del carattere jolly, l'asterisco *. Se non si ricorda il nome completo della funzione di cui si cercano spiegazioni, si può utilizzare anche solo una parte del nome, sostituendo la parte non nota con il carattere jolly *. Se ad esempio non si ricorda per esteso il nome Solve, basta scrivere:
![]()
![]()
Un aiuto, o meglio una facilitazione per la scrittura dei nomi delle funzioni, viene fornita dal front end attraverso il meccanismo del completamento automatico delle parole e delle espressioni. Dopo aver iniziato a scrivere parte del nome di una funzione si può digitare la sequenza di caratteri [CTRL] -[k]. Se esiste una sola parola riconosciuta da Mathematica che inizia con le stesse lettere digitate, allora viene automaticamente completata la parola; se, invece, vi sono più parole che iniziano con tali lettere, viene mostrato un riquadro con l'elenco di tali parole, da cui si può scegliere quella desiderata:
Per completare automaticamente la parola basta indicare con il puntatore del mouse la parola desiderata o selezionarla utilizzando le frecce di scorrimento della tastiera e digitare successivamente [RETURN].
Un'altra funzionalità del front end, di aiuto durante la scrittura dei comandi, è il completamento automatico dell'espressione, analoga alla precedente. Una volta completata la parola chiave, si può chiedere il completamento dell'espressione da utilizzare con la sequenza di tasti [SHIFT] [CTRL] -[k]. Questa funzionalità è molto utile, ad esempio, per i comandi di grafica, che solitamente richiedono una struttura dell'input abbastanza articolata. Provare a digitare [SHIFT] [CTRL] -[k] nella linea di input seguente:
![]()
Si noti che il completamento automatico del nome funziona anche per i simboli speciali, quelli che possono essere introdotti con la forma \[NomeSimbolo]. Si provi ad esempio a digitare [CTRL] -[k] nella linea seguente
![]()
Come ultima considerazione, si sottolinea che quanto fin qui detto a proposito dell'help in linea, ossia per i comandi ?, ??, [CTRL] -[k] e [SHIFT] [CTRL] -[k], vale sia per le funzioni native del sistema, sia per tutto quanto definito dall'utente.
I messaggi di errore
I messaggi di errore che Mathematica adotta sono numerosissimi e vengono raggruppati in diverse categorie, a seconda della tipologia di problema riscontrato (sintassi non corretta, problemi dell’algoritmo interno, mancanza di dati per la computazione, etc).
Si riporta di seguito una sequenza di operazioni esemplificative che mostra il differente comportamento del sistema, a seconda degli errori commessi. Si osservi cosa succede quando viene digitata una sequenza di caratteri totalmente insignificante dal punto di vista dei comandi di Mathematica.
![]()
![]()
Probabilmente ci si aspettava che il sistema restituisse un messaggio di errore e che non effettuasse alcuna operazione: è accaduto esattamente l'opposto!
In effetti, sebbene l'espressione non assuma nessun significato dal punto di vista dell'utente, per il kernel essa corrisponde ad un'operazione ben precisa e scritta correttamente dal punto di vista della sintassi, ossia corrisponde alla moltiplicazione delle variabili oiehof, wefo, wijogiesjgo, jfvg, dskfv e skdmòl per cui l'output riporta il risultato, ovviamente simbolico, della loro moltiplicazione. Si noti che l'ordinamento delle variabili viene eseguito automaticamente dalla funzione Times (moltiplicazione).
Cosa succede quando per caso si introduce, oltre alle lettere, qualche carattere a cui il sistema attribuisce un particolare significato?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Tralasciando per un momento l'interpretazione dei messaggi, si può intuire la differenza del comportamento del kernel rispetto all'esecuzione precedente. In questo ultimo caso tra le varie parole sono stati inseriti alcuni simboli, in particolare il punto . e la sequenza backslash + punto (/.). Il kernel, quindi, ha tentato di eseguire alcune operazioni associate a tali simboli, andando chiaramente in errore perché gli argomenti passati a tali funzioni non sono nella forma corretta.
Si riporta ora una serie di esempi in cui l'interpretazione dei messaggi guida l'utente ad individuare gli errori occorsi.
![]()
![]()
![]()
In questo caso il messaggio parla chiaramente di un errore nella scrittura dell'equazione, quindi va interpretato nel modo seguente: la funzione Solve è stata riconosciuta quindi la sua sintassi è corretta; è il suo argomento che non è scritto nel modo giusto perchè l'espressione ![]() non è affatto un'equazione ma una semplice espressione algebrica, mancando del simbolo che identifica le equazioni (==) ed il secondo membro dell'equazione stessa. In questo caso, il messaggio di errore suggerisce in maniera evidente la correzione da apportare.
non è affatto un'equazione ma una semplice espressione algebrica, mancando del simbolo che identifica le equazioni (==) ed il secondo membro dell'equazione stessa. In questo caso, il messaggio di errore suggerisce in maniera evidente la correzione da apportare.
Si supponga, invece, di scrivere la seguente espressione:
![]()
![]()
Questa volta il sistema non è in grado di stabilire se è stato commesso un errore di scrittura della parola Solve oppure se si voleva effettivamente utilizzare (o creare) una nuova funzione dal nome Solvi. Mathematica è anche un linguaggio di programmazione, quindi permette di definire nuove variabili e/o funzioni; questo spiega perché il sistema non riesce ad identificare con certezza una situazione di errore come nell’esempio.
Se l’intenzione era quella di calcolare le radici dell’equazione, ossia di utilizzare effettivamente la funzione Solve, verificando la sintassi della cella di input ci si rende conto che al posto della e si è scritta la i.
Infine, una volta eliminati tutti gli errori, si ottiene la risposta corretta:
![]()
![]()
Sintetizzando, gli esempi precedenti lasciano intuire che, nella maggior parte dei casi, il sistema è in grado di interpretare l'input, capire gli errori e quindi aiutare l'utente nella correzione tramite l'uso di messaggi appropriati. Si riportano altri esempi di messaggi.
Nella linea seguente manca una parentesi graffa di chiusura della lista delle equazioni del sistema da risolvere.
![]()
![]()
![]()
Si noti che alcune volte, soprattutto nel caso degli errori di sintassi, il messaggio di errore si conclude con un'espressione che replica l'input errato, sottolineata in rosso nella parte dove si è verificato l'errore. In tali casi non si ottiene alcun risultato come output, perché è il front end che effettua la verifica di correttezza della sintassi, ed in caso di errore non invia alcuna richiesta al kernel. Diversamente, come visto in precedenza, al verificarsi di errori di altra natura, il kernel risponde restituendo in output la stessa riga di comandi data in input. Il fatto che la riga di output sia la stessa di quella in input appare anche in altre circostanze, quando il kernel non è in grado di soddisfare le richieste anche se non vi sono errori. Ciò accade soprattutto con quelle funzioni chiamate macro-solutori, quali ad esempio Integrate, Solve, DSolve, etc. Infatti, in molti casi tali funzioni non sono in grado di computare alcuna risposta, o per via di limitazioni dell'algoritmo corrispondente o perché non esistono soluzioni per il calcolo richiesto. Ad esempio:
![]()
![]()
![]()
Il messaggio in questo caso non è tanto di errore quanto di attenzione nell'interpretazione della risposta fornita dal kernel.
![]()
![]()
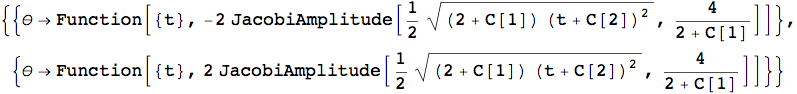
Infine, un'ultima considerazione sul modo in cui Mathematica supporta l'utente nella scrittura delle espressioni input. Quando si scrive un'espressione le parentesi aperte, per le quali non si è digitata ancora la corrispondente parentesi chiusa, vengono mostrate con un differente colore:
![]()
Se si dimentica di chiudere una parentesi ad un certo livello, tutte le parentesi ai livelli superiori rimarranno colorate, come nell'esempio che segue:
![]()
in cui, avendo dimenticato di inserire la parentesi graffa di chiusura della lista di equazioni, la successiva parentesi di chiusura della Solve rimane colorata in rosso, sebbene sia correttamente abbinata a quella di apertura. Questo suggerisce all'utente di verificare la correttezza dell'espressione prima di mandarla in esecuzione e generare un errore di sintassi.
![]()
![]()
![]()
![]()
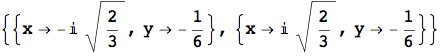
I principi fondamentali
Le parti di un’espressione
Come in tutti i linguaggi simbolici, in Mathematica uno degli aspetti fondamentali è quello del poter gestire le intere espressioni, o anche solo parti di esse. Dunque, come ci si aspetta, esistono diversi comandi per prelevare, modificare, sostituire e, in generale, manipolare le espressioni e le loro componenti. In questo paragrafo vedremo la funzione Part che serve a prelevare oggetti interni ad una espressione. Si consideri la seguente:
![]()
![]()
La lunghezza dell'oggetto assegnato alla variabile è pari al numero dei suoi argomenti, cioè 4. Con la funzione Part è possibile prelevare uno o più oggetti interni alla variabile. Le singole parti che compongono un'espressione sono raggiungibili mediante uno schema di indicizzazione molto semplice: ad ogni parte viene associato un numero che corrisponde all'indice del posto che essa occupa nell'espressione.
![]()
![]()
La rappresentazione sintetica per la funzione Part è data dalle parentesi quadre doppie [[ e ]], utilizzate, rispettivamente, per l'apertura e la chiusura. Pertanto, la sintassi dell'istruzione precedente è equivalente a:
![]()
![]()
Con la Part è possibile anche chiedere la parte di posto zero, che corrisponde alla head dell'espressione:
![]()
![]()
![]()
![]()
Come ci si aspetta, la Part non può essere utilizzata su oggetti atomici:
![]()
![]()
![]()
![]()
![]()
in quanto gli atomi non hanno una rappresentazione alternativa dalla quale sia possibile estrarre elementi interni, dunque hanno lunghezza zero.
Con la Part è possibile anche utilizzare la numerazione negativa, che considera l'espressione a partire dalla fine:
![]()
![]()
![]()
![]()
Opzioni
Le opzioni forniscono ulteriori informazioni ed argomenti alle funzioni per adattare i risultati alle specifiche esigenze dell'utente.
In senso generale, si può affermare che il meccanismo delle opzioni interviene in due momenti diversi: quando si utilizzano le funzioni di carattere prettamente computazionale, per indicare opportune informazioni aggiuntive all’algoritmo che deve risolvere un problema di calcolo; e, come nel caso della grafica e della programmazione del front end, quando si desidera personalizzare il modo in cui appare (layout) un oggetto. Si riportano di seguito alcuni esempi.
Quando si chiede un integrale definito mediante la funzione Integrate, Mathematica cerca di restituire un valore sempre valido indicando, se è necessario, le condizioni di validità.
![]()
![]()
Se il risultato ottenuto non è proprio come ci si aspettava, si può provare a visualizzare le opzioni della funzione Integrate, per tentare di modificarne il comportamento. Per sapere le opzioni di un oggetto si può procedere in due modi: utilizzando il ?? o il comando Options
![]()
| Attributes[Integrate]={Protected,ReadProtected} | |
|
![]()
![]()
Se si vuole conoscere l'uso ed il significato di una particolare opzione, basta utilizzare uno degli help disponibili.
![]()
| Attributes[Assumptions]={Protected} |
Dunque, l'opzione Assumptions permette di indicare a priori le condizioni, se note, sui parametri. Se si è interessati ai soli valori reali minori di zero del parametro a basta indicare tale condizione mediante l'opzione Assumptions.
![]()
![]()
In questo caso, lo stesso risultato si ottiene impostando il valore False per l'opzione GenerateConditions.
![]()
![]()
In pratica le Option sono delle condizioni interne agli algoritmi associati alle varie funzioni, e pertanto devono sempre avere un valore definito. Questo conduce facilmente al concetto del valore di default per ciascuna Option, che viene impostato dal sistema ed utilizzato dal kernel nel caso in cui l'utente ometta le indicazioni in merito. Segue ancora un esempio di opzioni nel caso della funzione Limit.
![]()
![]()
![]()
![]()
![]()
| Attributes[Direction]={Protected} |
Come si legge dal messaggio di help precedente, se si desidera specificare la direzione con cui la variabile indipendente tende al valore limite, basta utilizzare l'opzione Direction:
![]()
![]()
![]()
![]()
Anche per la Limit, in alcuni casi si rende indispensabile l'utilizzo dell'opzione Assumptions per ottenere un risultato corretto:
![]()
![]()
![]()
![]()
![]()
![]()
L'altro caso in cui si può influenzare il comportamento del sistema tramite il meccanismo delle opzioni è quello della grafica o del front end. La tabella che segue mostra alcune opzioni inerenti le principali funzioni di grafica in due e tre dimensioni (d'ora in poi indicata come 2D e 3D).
Nome
Default
Descrizione
![]()
![]()
Rapporto tra altezza e larghezza del grafico
![]()
True
Disegna o meno gli assi
![]()
None
Etichette sugli assi
![]()
Automatic
Origine degli assi
![]()
Automatic
Colore dello sfondo
![]()
Automatic
Tacche delle unità di misura sugli assi
![]()
25
Numero di punti campione da usare
Si mostrano ora alcuni esempi di modifica del risultato grafico ottenuto con Plot.
![]()
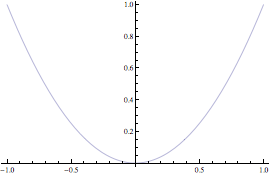
![]()
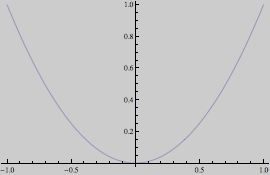
![]()
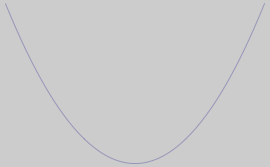
Attributi
Mentre le opzioni di una funzione offrono la possibilità di variare il suo comportamento in funzione del valore ad esse assegnato, gli attributi di una funzione indicano alcune sue caratteristiche preimpostate, che possono essere inibite, ma non modificate nella loro influenza sul comportamento della funzione stessa.
Constant
Se si vuole calcolare la derivata di un'espressione con variabili e parametri, potrebbe essere utile indicare i parametri come costanti rispetto alla variabile indipendente, ossia a derivata nulla.
![]()
![]()
A meno di opportune specifiche sul parametro c, Mathematica indica il risultato della precedente derivata in funzione della derivata di c rispetto ad x, essendo c non definito. Se c deve essere inteso come costante, basta impostare per essa l'attributo Constant.
![]()
![]()
![]()
Protected
L'attributo Protected, assegnato di default a tutti gli oggetti nativi di Mathematica, serve per prevenire eventuali ri-assegnazioni di simboli o funzioni protette. Ad esempio potrebbe capitare di voler utilizzare le variabili D o I, che sono, rispettivamente, il simbolo di derivata parziale e di unità immaginaria.
![]()
![]()
![]()
![]()
![]()
![]()
Come richiamato dai messaggi di errore, tali simboli hanno l'attributo Protected, che evita appunto eventuali assegnazioni dell'utente che potrebbero causare malfunzionamenti al sistema. Ovviamente anche per le proprie routine o variabili si può impostare l'attributo Protected, così da evitare errori involontari da parte di chi poi le utilizza.
Un simbolo protetto non può essere né modificato (assegnazione di un altro valore), né cancellato (rimozione del valore assegnato), né rimosso (eliminazione definitiva dalla sessione corrente).
L'attributo Protected offre la possibilità di rimuovere la protezione di un oggetto tramite la funzione Unprotect.
![]()
![]()
![]()
![]()
![]()
|
![]()
![]()
![]()
Rendere permanente il valore di un’opzione
Si individuano tre livelli distinti di validità delle modifiche apportate alle opzioni:
a) livello locale, validità per il solo oggetto cui si associa l’opzione;
b) livello di sessione corrente, validità per la sessione di kernel attuale, scompare alla chiusura del kernel;
c) livello globale, ossia valido per tutte le sessioni di Mathematica.
Se si vuole un particolare colore di sfondo per un grafico basta scrivere:
![]()
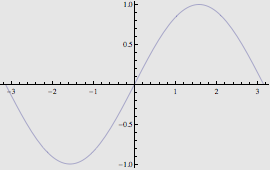
In questo caso la modifica avrà validità solo per l’oggetto appena creato, quindi è locale all’oggetto stesso (caso a). Invece, se si desidera che per la sessione corrente di Mathematica (caso b) i grafici abbiano tutti lo stesso colore di sfondo, si può impostare GrayLevel[0.9] come valore di default per l’opzione Background con il comando SetOptions:
![]()

D'ora in poi tutti i grafici avranno lo sfondo grigio senza che ciò debba essere specificato esplicitamente come opzione nella chiamata della Plot.
![]()
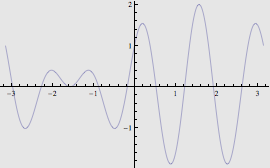
![]()

Questa impostazione per il Background della Plot rimarrà valida fino a quando non si chiude la sessione corrente (chiusura del solo kernel o del sistema Mathematica) o fino a quando non si applica una nuova modifica tramite la SetOptions. Ovviamente anche dopo l'utilizzo della SetOptions è possibile modificare localmente un grafico:
![]()

![]()

Per ripristinare il valore di default per l'opzione Background della Plot digitare:
![]()
![]()
Infine, per rendere una modifica valida per tutte le sessioni di Mathematica, si deve modificare il file di inizializzazione del sistema denominato init.m (su Mac il file si trova nel percorso /Library/Mathematica/Kernel).
Elementi di base
Le liste
Alcuni linguaggi di programmazione adottano un tipo di dati differenziato per vettori, matrici e liste. In Mathematica non si ha una vera e propria distinzione tra le varie strutture dati, essendo tutte viste generalmente come liste. Una lista può contenere qualsiasi cosa, ed in qualsiasi ordine e livello di nidificazione. Il criterio generale è che Mathematica vede una qualsiasi lista come una struttura dati anche quando la sua forma è compatibile con il significato di un vettore, di una matrice o un tensore. Pertanto, soprattutto nell’applicazione delle funzioni del calcolo matriciale è opportuno prestare attenzione ai risultati. Più avanti, in questo paragrafo, si riprenderà tale concetto riportando alcuni esempi.
Costruzione di liste
In Mathematica la struttura dati più comune e più utile è proprio la List, un elenco di elementi (espressioni composte o atomi) delimitato dalle parentesi {}. Per costruire una lista si possono utilizzare diversi metodi. Ad es. scrivendo direttamente gli elementi racchiusi tra le parentesi:
![]()
![]()
Oppure si può scrivere:
![]()
![]()
![]()
Le espressioni precedenti indicano al sistema di creare un oggetto di tipo lista con dentro le cifre da 0 a 9; per separare gli oggetti all'interno di una lista bisogna utilizzare la virgola. La lista può essere vista come un contenitore di oggetti: all'interno di una lista si possono inserire numeri, variabili, simboli, funzioni, operatori, o anche altre liste ancora.
![]()
![]()
Nella lista precedente sono stati inseriti dei numeri, delle costanti, delle stringhe, un'equazione ed una lista. Per creare una lista si possono adoperare diverse funzioni. Il modo più immediato e semplice per costruire le liste è mediante l’utilizzo della funzione Table.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()

![]()
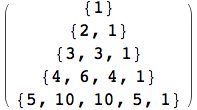
Il comando Range genera una lista di numeri compresi in un intervallo specificato. Per default il minimo è considerato 1.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Anche la funzione Array serve per creare liste o liste di liste:
![]()
![]()
Allo stesso modo, se si indica una coppia di valori, si può creare una matrice anziché un vettore:
![]()

La funzione Array offre anche l’opportunità di modificare il risultato ottenuto, sostituendo la head List con un’altra head, quindi utile per generare anche espressioni diverse dalle liste.
![]()
![]()
![]()
![]()
La funzione SparseArray risulta molto utile nella creazione di liste laddove esse rappresentano matrici con un elevato numero di elementi nulli. Infatti, SparseArray permette di creare matrici sparse specificando solo gli elementi non nulli. Per default, gli elementi non specificati vengono impostati a zero, ma volendo si può modificare tale impostazione.
![]()
![]()
![]()
![]()
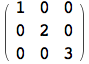
![]()
![]()
La differenza enorme tra le due forme è che nel primo caso si ha una forte riduzione di spazio di memoria necessario per conservare la matrice, pur mantenendo tutte le informazioni necessarie per operare su di essa. Ovviamente, per piccole matrici tale vantaggio può sembrare banale, ma basta considerare una matrice 100×100 per comprenderne la reale potenzialità.
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Infine, un'altra funzione molto utile relativamente alla manipolazione delle liste è la Flatten, che elimina i livelli di parentesi nelle liste di liste. Ad esempio:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Oppure, mettendo tutto insieme nel calssico stile della programmazione funzionale:
![]()
![]()
Un altro caso frequente ricorre quando si uniscono diverse liste tramite Join:
![]()
![]()
![]()
![]()
Data la seguente lista:
![]()
![]()
per ottenere l'elemento stringa, il quarto elemento della lista, bisognerà scrivere:
![]()
![]()
oppure
![]()
![]()
Data la seguente lista:
![]()
si supponga di voler prendere gli elementi 4 e 6 che si trovano nella seconda sottolista alle posizioni 1 e 3, rispettivamente. Un modo di procedere potrebbe essere:
![]()
![]()
In maniera più sintetica, si può scrivere :
![]()
![]()
Altro esempio: si estraggano dalla lista lista le righe 1 e 3
![]()
![]()
Infine, se si desidera prendere una sola colonna dalla matrice memorizzata in lista, basta scrivere:
![]()
![]()
![]()

L’attributo Listable
E’ possibile eseguire operazioni aritmetiche direttamente sulle liste, come negli esempi che seguono:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Se si desidera conoscere il valore nel punto x=0 delle derivate delle espressioni sopra calcolate si può scrivere:
![]()
![]()
Esportazione
Quando bisogna esportare dati in un particolare formato, ad esempio per problemi di compatibilità con altre applicazioni, bisogna utilizzare la Export. I formati riconosciuti sono indicati dalla variabile $ExportFormats.
![]()

Ad esempio, vediamo come esportare una lista di valori in formato CSV, compatibile con Excel.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2,3,5,3,5
4,3,2,5,5
3,4,1,4,3
3,3,2,4,4
4,3,5,2,4
![]()
![]()
![]()
{2, 3, 5, 3, 5}
{4, 3, 2, 5, 5}
{3, 4, 1, 4, 3}
{3, 3, 2, 4, 4}
{4, 3, 5, 2, 4}

![]()
![]()
%% AMS-LaTeX Created by Wolfram Mathematica 8.0 : www.wolfram.com
\documentclass{article}
\usepackage{amsmath, amssymb, graphics, setspace}
\newcommand{\mathsym}[1]{{}}
\newcommand{\unicode}[1]{{}}
\newcounter{mathematicapage}
\begin{document}
\[\sqrt{\frac{x^2}{(-1+x)^2}}\]
\end{document}
Tramite la Export si possono convertire anche interi documenti, oltre che singole espressioni.
I macro-solutori
Una delle caratteristiche di Mathematica che lo hanno reso utile ed indispensabile in molti contesti scientifici è la disponibilità di un ampio insieme di macro solutori, ossia funzioni in grado di risolvere, con una sola istruzione, problemi complessi come, ad esempio, il calcolo analitico di un integrale, un limite o un sistema di equazioni differenziali. La tabella che segue riporta un elenco dei macro solutori più frequentemente utilizzati.
Nome
Descrizione
![]()
Soluzione di equazioni o sistemi
NSolve
Soluzione di equazioni o sistemi con metodi numerici
![]()
Soluzione con metodi analitici di equazioni differenziali o sistemi
![]()
Soluzione con metodi numerici di equazioni differenziali o sistemi
![]()
Integrazione con metodi analitici
![]()
Integrazione con metodi numerici
![]()
Calcolo di limiti
![]()
Sviluppo in serie di potenze
D
Derivata parziale
Dt
Derivata totale
Derivata (parziale D, totale Dt)
Oltre alla potenzialità di calcolo, tali macro solutori offono, alle volte, un ulteriore aiuto. Operando nel caso simbolico, essi permettono di esplorare le regole generali che si applicano ai vari calcoli. Ad esempio, nel caso dell’operatore di derivata D, la sua caratteristica di operare anche in maniera simbolica, permette di rivedere le regole generali per il calcolo delle derivate. Chiamando la funzione D con una qualsiasi espressione e/o composizione di funzioni, senza peraltro specificare l’espressione analitica delle funzioni stesse, si ottiene la forma generale della derivata.
![]()
![]()
![]()
![]()
![]()
![]()
In questo ultimo caso la forma data in output potrebbe essere diversa da quella usualmente nota ma, volendo, si può ricondurla a quella tipica tramite l'uso del comando Together che riscrive un'espressione algebrica di più razionali in un'unica espressione con denominatore comune.
![]()
![]()
![]()
![]()
![]()
![]()
Per calcolare le derivate successive alla prima, basta indicare la variabile indipendente in una lista, il cui secondo argomento è l'ordine di derivazione:
![]()

Anche la funzione Integrate è in grado di operare su espressioni del tutto simboliche. Si provi a calcolare due volte l'integrale del risultato precedente.
![]()
![]()
![]()
![]()
Seguono altri esempi di derivate.
![]()
![]()
![]()
![]()
![]()

Alle volte può essere utile rivedere il risultato con la notazione scientifica tradizionale. Per fare ciò basta aggiungere, dopo il comando, una specifica di visualizzazione di tipo TraditionalForm:
![]()

Solve e Reduce
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| Attributes[DSolve]={Protected} | |
|

![]()
![]()

![]()
![]()
| Attributes[NDSolve]={Protected} | |
|
![]()
![]()
![]()
Uso evoluto di macro-solutori
Ora seguono altri esempi che illustrano situazioni abbastanza frequenti in Mathematica, ossia casi in cui i macro solutori non sono in grado, apparentemente, di fornire una risposta a determinati input. Il concetto sottostante è che molte volte prima di usare una funzione c'è bisogno di manipolare i dati di partenza in maniera tale da riscriverli in una forma non necessariamente più semplice, ma sicuramente più adatta e riconoscibile dagli algoritmi interni ai macro solutori.
Il primo esempio mostra il caso di un limite di una funzione che comprende un coefficiente binomiale.
Sia data la funzione 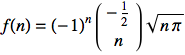 . Andando a calcolare una sequenza di punti della f(n) e visualizzandoli con la funzione ListPlot, si osserva graficamente che essa tende ad 1 per n che tende ad ∞.
. Andando a calcolare una sequenza di punti della f(n) e visualizzandoli con la funzione ListPlot, si osserva graficamente che essa tende ad 1 per n che tende ad ∞.
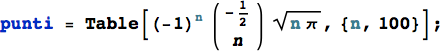
![]()
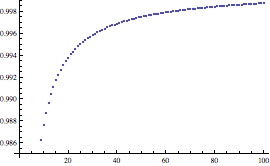
Se si tenta di calcolare tale limite direttamente con la funzione Limit, si osserva che essa non è in grado di fornire una risposta.

![]()
Occorre, dunque, tentare di riscrivere l'espressione della f(n) in maniera differente, applicando qualche regola teorica che permetta la semplificazione della sua espressione. Un primo passo è quello di utilizzare la funzione FunctionExpand che modifica l'espressione fornita, mediante l'applicazione di regole e funzioni speciali. In questo caso, FunctionExpand tenta di sostituire il coefficiente binomiale con una combinazione di funzioni Gamma di Eulero Γ(n).
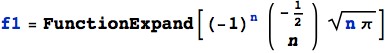
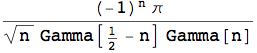
Il passo successivo sarà quello di semplificare ulteriormente tale risultato applicando la formula: Γ(n) Γ(1-n) = π csc(π n)
Per applicare tale formula, si utilizza la funzione ReplaceAll. In particolare, per sostituire il termine ![]() si moltiplica e divide per
si moltiplica e divide per ![]() . In tal modo comparirà il termine Γ(n)Γ(1-n) che potrà essere semplificato mediante l'uso della funzione FullSimplify.
. In tal modo comparirà il termine Γ(n)Γ(1-n) che potrà essere semplificato mediante l'uso della funzione FullSimplify.

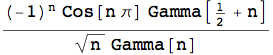
Ora si semplifica ulteriormente tale risultato, mediante la funzione Simplify con la specifica che n ∈ Z.
![]()

A questo punto si prova a calcolare il limite per n che tende ad infinito:
![]()
![]()
Come si vede dal risultato ottenuto, se ci si ferma ad un uso immediato dei macro solutori con i dati disponibili in partenza, si potrebbe erroneamente pensare che Mathematica non sia in grado di manipolare espressioni complesse. Viceversa, andando ad indagare sulle possibili rappresentazioni alternative dei dati disponibili, spesso mediante l’applicazione di regole teoriche o di funzioni di semplificazione disponibili quali, ad esempio, Simplify, FullSimplify, FunctionExpand, PowerExpand, ComplexExpand, etc. si ottiene il risultato desiderato.
Seguono altri esempi, sull’utilizzo dell’opzione Assumptions e sulle notevoli capacità, per i macro solutori, in merito alla specifica del dominio di appartenenza delle variabili o di particolare condizioni su di esse.
![]()
![]()

![]()
Un metodo alternativo per impostare una condizione su un argomento viene fornito dalla funzione Assuming. La comodità di tale alternativa è che si può specificare una sola volta la condizione su una variabile e poi far seguire una serie di calcoli, con chiamate a diversi macro solutori, che considereranno tutti la stessa condizione impostata.
L’esempio che segue imposta la condizione σ > 0, poi calcola l’integrale della funzione ![]()
![]() ed infine il limite del risultato ottenuto dall’integrale, per y che tende ad infinito. Infine, si aggiunge una lista con la funzione ed il limite come valori da restituire alla fine del calcolo.
ed infine il limite del risultato ottenuto dall’integrale, per y che tende ad infinito. Infine, si aggiunge una lista con la funzione ed il limite come valori da restituire alla fine del calcolo.

![]()
N.B. ![]() è l’integrale della distribuzione Gaussiana, dato da
è l’integrale della distribuzione Gaussiana, dato da ![]() .
.
Un'altra funzione analoga alla Assuming è Refine[espressione, ipotesi], che restituisce la forma che assume l'espressione se i simboli in essa compresi vengono sostituiti da valori che soddisfano le ipotesi. Ad esempio, risulta spesso utile impostare alcune condizioni per le variabili che compaiono in espressioni irrazionali.
![]()
![]()
Se è noto che la variabile x è sempre maggiore di zero, si può trasformare l'espressione di var.
![]()
![]()
Se anche y è maggiore di zero:
![]()
![]()
![]()
![]()
Anche la funzione Reduce rientra nella categoria dei macro solutori. Tale funzione, spesso utilizzata in alternativa alla Solve, riscrive l'espressione data in input cercando di risolvere le equazioni e disequazioni in essa presenti ed eliminando i quantificatori eventualmente presenti. In pratica, la Reduce può tornare molto utile per risolvere equazioni e sistemi di equazioni con l'aggiunta di specifiche condizioni sui parametri e sulle variabili.
![]()
![]()
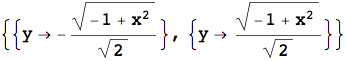
Il risultato fornito da Solve non tiene in considerazione alcuna ipotesi sul dominio cui appartengono le variabili, né permette di specificarlo in alcun modo. Con la Reduce, invece, è possibile indicare, ad esempio, il dominio di una o di tutte le variabili. Il comando che segue imposta nella Reduce tutte le variabili come reali.
![]()

![]()
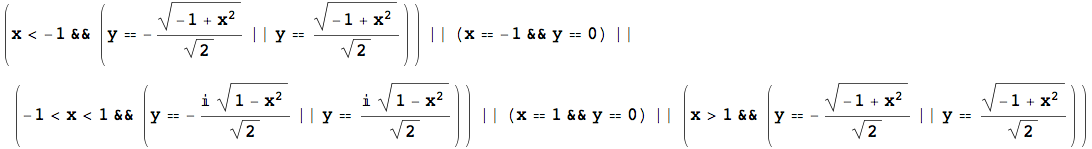
L'output generato da Reduce può essere riscritto come un'unica sequenza di soluzioni alternative (legate dall'operatore logico OR espresso con il simbolo ||), applicandovi la funzione LogicalExpand.
![]()
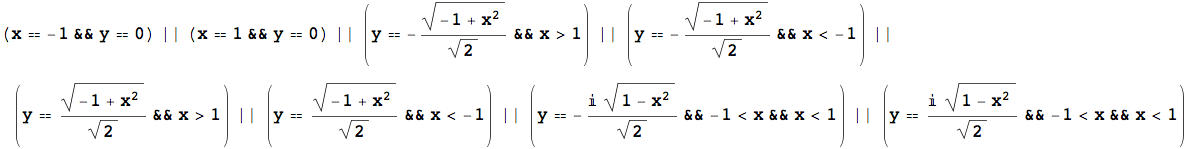
Nel caso di equazioni con parametri la Reduce è in grado di fornire anche indicazioni in merito ai parametri, laddove la Solve non esplicita alcuna considerazione e restituisce un risultato che, sotto certe condizioni, potrebbe anche perdere di significato.
![]()
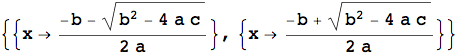
Nulla viene detto dalla Solve in merito a cosa accade alla soluzione se il parametro a è uguale a zero. La Reduce risponde allo stesso input evidenziando anche tale situazione.
![]()

L'esempio che segue mostra ancora una volta l'importanza del calcolo simbolico, in particolare nello studio di equazioni letterali. L'introduzione della LogicalExpand, della Apply e della TableForm servono unicamente per visualizzare il risultato in una forma più leggibile.
![]()
| a==0&&c==0&&x==0&&b>0 |
| a==0&&c==0&&x==0&&b<0 |
 |
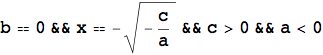 |
 |
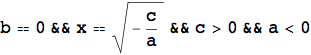 |
 |
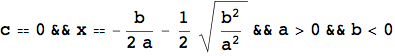 |
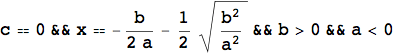 |
 |
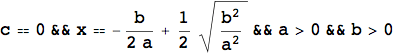 |
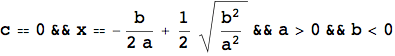 |
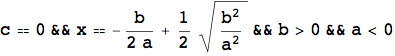 |
 |
 |
 |
 |
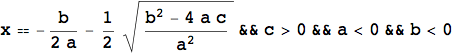 |
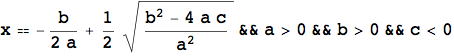 |
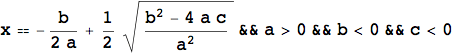 |
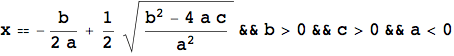 |
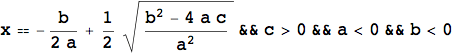 |
 |
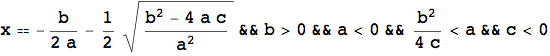 |
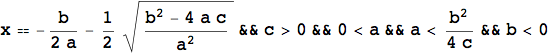 |
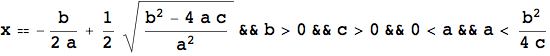 |
 |
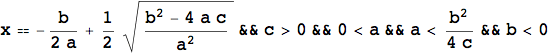 |
 |
 |
Ora si risolve nuovamente l'equazione ![]() nel caso di x, y ∈ Z. In questo caso si tratta di equazioni diofantinee. L'esempio seguente mostra una forma speciale chiamata equazione di Pell.
nel caso di x, y ∈ Z. In questo caso si tratta di equazioni diofantinee. L'esempio seguente mostra una forma speciale chiamata equazione di Pell.
![]()
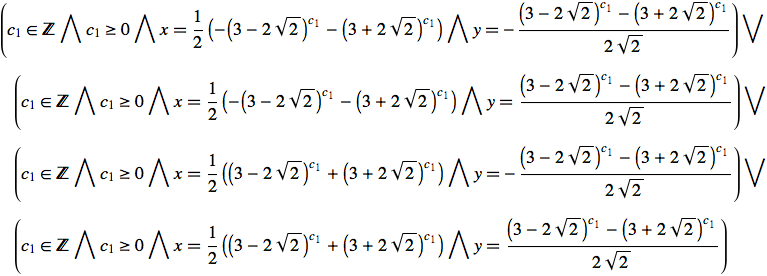
Un altro caso di equazione di Pell.
![]()

L'equazione di Thue.
![]()
![]()
Un altro caso importante in cui la Reduce si distingue dalla Solve è quello in cui si presentano soluzioni multiple, tipicamente con le equazioni goniometriche.
![]()
![]()
![]()
Come si legge dal messaggio generato da Solve, in questi casi viene espressamente suggerito di utilizzare la Reduce.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Un altro tipo di equazione che la Reduce è in grado di trattare è quello che comprende i quantificatori come ad esempio quello esistenziale (∃) e quello universale (∀), definiti da Mathematica rispettivamente con i termini Exists (∃) and ForAll (∀).
L'esempio mostra la determinazione dei valori di a e b che verificano la disuguaglianza per tutti i valori reali della x.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Come visto negli esempi precedenti, la Reduce restituisce la soluzione generica con tutte le condizioni sulle variabili e sui parametri. Spesso risulta utile conoscere una o più soluzioni numeriche per una determinata equazione o sistema. A tale scopo, è stata introdotta la funzione FindInstance che accetta gli stessi input della Reduce ma restituisce un numero, indicato dall'utente, di possibili soluzioni. FindInstance lavora su tutti i problemi per i quali la Reduce è in grado di restituire soluzioni complete. Il vantaggio di FindInstance è duplice: in alcuni casi è in grado di individuare soluzioni per problemi che Reduce non riesce a risolvere; l'individuazione di soluzioni numeriche riduce notevolmente i tempi di esecuzione.
L'esempio seguente mostra il calcolo delle radici dell'equazione ![]() .
.
![]()

Con FindInstance si richiede di individuare tre coppie di soluzioni numeriche dell'equazione sopra riportata.
![]()
![]()
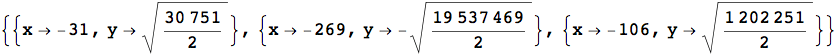
La funzione FindRoot è in grado di risolvere anche equazioni di variabili vettoriali e matriciali. Si risolve, ad esempio, l'equazione di Riccati in forma matriciale, la cui espressione analitica è ![]()
![]()
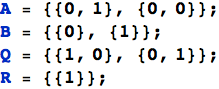
Il comando seguente trova la matrice radice dell'equazione data:
![]()
![]()
La funzione DSolve è anche in grado di individuare tutte le soluzioni razionali di un sistema di equazioni lineari con coefficienti razionali e può risolvere i sistemi lineari di equazioni differenziali con coefficienti costanti.
L'esempio che segue mostra la soluzione di un sistema di equazioni differenziali i cui coefficienti sono funzioni razionali e la cui soluzione è razionale.
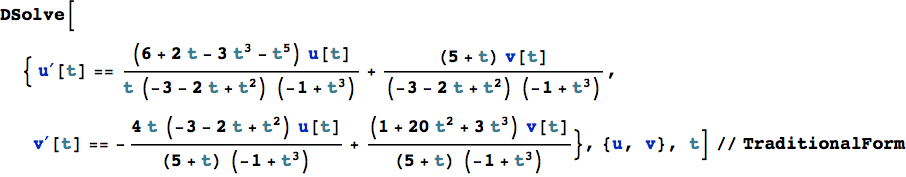
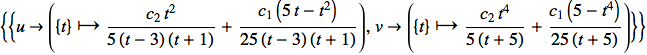
Nella seguente equazione algebrico-differenziale DSolve restituisce una soluzione generale con un solo parametro, sebbene sia un sistema di ordine due. Un grado di libertà viene rimosso per via dell'equazione algebrica che lega le variabili.
![]()
![]()
In questo caso si ha la libertà di scegliere un solo valore iniziale con valore arbitrario:
![]()
![]()
Quello che segue è il valore iniziale implicato dal valore iniziale dell'altra variabile:
![]()
![]()
![]()
Infine, si riportano alcuni esempi della nuova funzione RSolve, che risolve sistemi di equazioni alle differenze lineari e non lineari, equazioni algebriche alle differenze ed equazioni alle differenze con derivate parziali. Proprio come nel caso di equazioni differenziali, le equazioni alle differenze anche se appaiono semplici, potrebbero generare soluzioni molto complicate, e non ci sono funzioni abbastanza generali per esprimere tutte le soluzioni in forma chiusa. In molti casi, comunque, tali soluzioni possono essere trovate, come negli esempi che seguono.
Equazione alle differenze per i polinomi di Legendre.
![]()
![]()
Equazione ![]() con una costante arbitraria
con una costante arbitraria ![]() .
.
![]()
![]()
Equazione alle differenze ![]() con l'equazione iniziale
con l'equazione iniziale ![]()
![]()
![]()
Si risolve un'equazione alle differenze del secondo ordine con due condizioni al contorno.
![]()
![]()
È possibile visualizzare graficamente la soluzione con un tipico diagramma stem (diagramma a rami). Si noti che s è stata determinata senza utilizzare la funzione TraditionalForm che ne avrebbe impedito il successivo utilizzo.
![]()

Questo esempio mostra la soluzione dell'equazione lineare del secondo ordine con coefficienti variabili: ![]() .
.
![]()
![]()
Si risolve ora un sistema lineare di equazioni alle differenze e equazioni algebriche. Si noti che questo sistema ha solo una costante generale nella soluzione, poiché un grado di libertà è stato rimosso dall'equazione algebrica.
![]()
![]()
Di seguito si riporta il problema del valore iniziale con un solo valore iniziale assegnato:
![]()
![]()
Questo è il valore iniziale di y:
![]()
![]()
Le equazioni alle differenze parziali hanno diverse variabili indipendenti. In tali casi, la soluzione generale è ottenuta parametrizzando la funzione generale.
Segue un esempio di equazione alle differenze parziali lineare, con una funzione arbitraria generale C[1] [l -k].
![]()
![]()
Alcune operazioni con le matrici
Nei paragrafi precedenti si è parlato genericamente di liste; in alcuni casi si è già introdotta l'interpretazione delle liste come vettori o matrici. Se una lista assume una forma particolare, ad esempio se si tratta di una lista di liste e tutte queste sono della stessa dimensione, allora si può attribuire il significato di matrice a tale struttura, e su di essa si possono eseguire le comuni operazioni appartenenti all'algebra delle matrici.
Come concetto generale, non bisogna mai dimenticare che per Mathematica una lista è una struttura dati, ancor prima di assumere significato di vettore o matrice. Questo significa che alcune operazioni possono essere svolte anche se dal punto di vista teorico non sono ammissibili. Ad esempio, sebbene l'operazione di divisione tra matrici non è definita, in Mathematica è possibile dividere due matrici. Tale operazione, come mostra l'esempio che segue, assume un significato solo dal punto di vista delle liste.
![]()
![]()

![]()
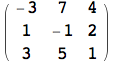
![]()
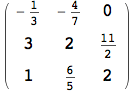
In questo caso, seppure i due oggetti di tipo lista A e B possono essere considerati come matrici, Mathematica li considera come strutture dati sui quali l'utente ha chiesto di eseguire l'operazione di divisione. Sarà l'utente a dover intendere questa operazione come la creazione di una lista di liste i cui elementi sono dati dalla divisione degli elementi di posto omologo delle due liste A e B e non come l'operazione di divisione tra le due matrici A e B. Mathematica esegue sempre le operazioni aritmetiche su liste di forma compatibile, applicando l'operazione sui termini di posto omologo. Infatti, oltre alla divisione, anche le altre operazioni aritmetiche assumono lo stesso significato sulle liste. Ad esempio, la moltiplicazione eseguita con l'operatore * o equivalentemente con il carattere blank (lo spazio) assume il significato di moltiplicazione degli elementi di posto omologo e non di prodotto matriciale, il quale si ottiene con la funzione Dot, rappresentata in forma breve con il punto .
![]()
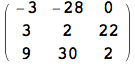
![]()
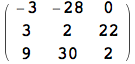
![]()
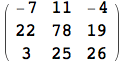
![]()

![]()

![]()

Ovviamente, se le due liste non hanno una forma compatibile viene restituito un messaggio di errore.
![]()
![]()
![]()
Mathematica mette a disposizione numerose funzioni per la manipolazione di matrici. La tabella che segue ne riporta un breve elenco.
Funzione
Descrizione
![]()
l'inversa
![]()
il determinante
![]()
la trasposta
![]()
la traccia
![]()
gli autovalori
![]()
gli autovettori
![]()
gli autovalori e gli autovettori
![]()
il polinomio caratteristico
![]()
il rango
Si noti che in Mathematica non c'è differenza tra un vettore riga ed un vettore colonna, in quanto le funzioni che operano su vettori e matrici automaticamente individuano la forma appropriata in base all'input fornito. Se si deve moltiplicare la matrice A a sinistra per un vettore riga ed a destra per un vettore colonna, basta scrivere:
![]()
![]()
Il prodotto scalare di due vettori viene eseguito dalla funzione Dot:
![]()
![]()
mentre la funzione Cross (oppure l’operatore ×) esegue il prodotto vettoriale:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
La funzione Norm restituisce la norma di un vettore:
![]()
![]()
![]()
![]()
Più volte in precedenza si è utilizzata la visualizzazione in forma matriciale di una lista di liste, tramite la funzione MatrixForm. Bisogna prestare attenzione alle forme di visualizzazione disponibili in Mathematica, in quanto non devono mai essere utilizzare quando si assegna il valore ad una variabile. Si consideri il seguente esempio:
![]()

![]()
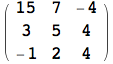
![]()
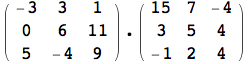
![]()
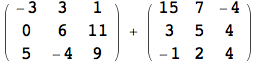
![]()
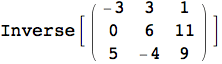
Il risultato è inaspettatamente privo di significato, ossia viene visualizzata l'operazione richiesta, ma non viene eseguito alcun calcolo. Il motivo è collegato al modo in cui si sono memorizzate le due matrici.
![]()
![]()
![]()
![]()
cioè esse sono oggetti di tipo MatrixForm e non List, dunque le operazioni sulle liste non sono applicabili. La MatrixForm ha significato unicamente per quanto attiene la visualizzazione del front end della lista in forma di matrice, ma non per la sua interpretazione dal punto di vista delle strutture dati. Infatti, MatrixForm funziona in generale su qualsiasi lista, anche se essa non rappresenta una matrice. Quella che segue è banalmente una lista ma non una matrice, ciò non toglie che sia possibile utilizzare la MatrixForm su di essa:
![]()

Pertanto, bisogna ricordarsi di non utilizzare mai la MatrixForm quando si definisce una matrice e la si assegna ad una variabile. È preferibile utilizzarla solo quando si chiede di visualizzare le matrici o il risultato di una operazione su di esse.
![]()
![]()
![]()
![]()
![]()
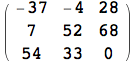
![]()
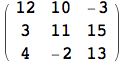
Ritornando all'utilità della MatrixForm, quando si lavora con le matrici, se si desidera visualizzare sempre i risultati in forma tradizionale, si può impostare la variabile d'ambiente $Post come segue:
![]()
![]()
Da questo punto in avanti, tutti gli output sotto forma di liste verranno rappresentati automaticamente come matrici.
![]()
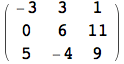
![]()
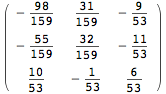
Anche per le operazioni sulle matrici può tornare utile, alle volte, sfruttare il calcolo simbolico per visualizzare regole generali. Ad esempio, per mostrare come si ottiene il prodotto di due matrici si può procedere nel seguente modo.
Si creano due matrici simboliche usando la funzione Array e poi si esegue il loro prodotto.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
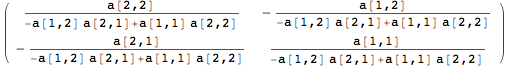
![]()
![]()
![]()

![]()

La funzione MatrixPlot è molto utile per sintetizzare la struttura di una matrice mediante una rappresentazione grafica dei suoi elementi.

![]()

Il risultato ottenuto in questo caso, evidenzia come la matrice M sia una matrice a blocchi, infatti le aree in bianco nel grafico indicano i blocchi con elementi nulli. Se si aggiunge l'opzione Mesh, si evidenzia maggiormente la struttura di righe e colonne.
![]()

La MatrixPlot risulta maggiormente significativa per la visualizzazione di struttura per matrici molto grandi, come negli esempi che seguono.
![]()
![]()
![]()
![]()
![]()
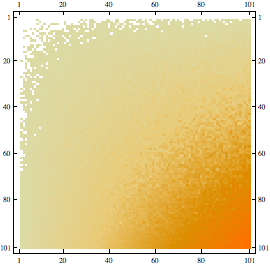
![]()
![]()
![]()
![]()
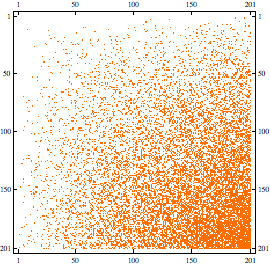
Riducendo il numero di elementi da visualizzare è possibile anche evidenziare con diverse tonalità di grigio densità degli elementi non nulli.
![]()
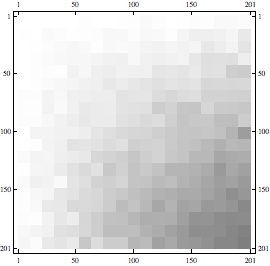
Matrici sparse
Come ultimo argomento, esaminiamo la gestione ottimizzata per le matrici sparse, già brevemente introdotte in precedenza. Un elevato numero di problemi reali si affronta con modelli matematici che presentano matrici sparse, ossia matrici dove la maggior parte degli elementi sono nulli. La gestione di tali matrici in Mathematica è totalmente integrata con le altre funzionalità del sistema e permette di lavorare con array di qualsiasi dimensione. Questo significa che una volta definita una matrice con l'apposita funzione SparseArray si possono utilizzare tutte le altre funzioni.
Per creare una matrice o vettore sparso, bisogna usare la funzione SparseArray, la cui struttura più comune è la seguente: SparseArray[regole, dimensione]
![]()
Il meccanismo delle regole permette di semplificare la creazione di particolari tipi di matrici. Infatti, per alcuni tipi di matrice, ad esempio quelle diagonali o triangolari, gli elementi non nulli sono disposti su particolari posizioni della matrice. Se, oltre alla posizione, anche il loro valore può essere determinato mediante una particolare funzione, allora conviene costruire una regola che a partire dagli indici di posizione i e j calcola automaticamente i valori delle entrate.
Ad esempio, per costruire la matrice identità basta scrivere:
![]()
![]()
Come si osserva dall'output, l'oggetto generato è di tipo SparseArray e non lista. Gli SparseArray vengono gestiti dalle funzioni native come una lista di liste. L'utente non deve farsi carico di specificare alcuna informazione nel trattare tali oggetti come se fossero una vera e propria matrice.
![]()
![]()
![]()
![]()
![]()
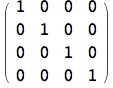
![]()

![]()
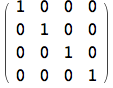
![]()

Se si desidera convertire un oggetto di tipo SparseArray in una lista, si può utilizzare la funzione Normal.
![]()
![]()
Se si desidera conoscere le regole interne di una matrice sparsa, si può utilizzare la funzione ArrayRules.
![]()
![]()
Si noti che, anche se esiste il comando IdentityMatrix che genera matrici identità di qualsiasi dimensione, se le dimensioni della matrice sono notevoli è comunque preferibile usare la sua rappresentazione nella forma SparseArray.
Si calcola il numero di byte per memorizzare una matrice identità di dimensioni 1000×1000 in entrambi i modi.
![]()
![]()
![]()
![]()
![]()
![]()
Per quanto concerne i tempi di calcolo, in alcuni casi non si registrano notevoli differenze tra le due forme di memorizzazione.
![]()
![]()
![]()
![]()
Una possibile risposta è che la forma sparsa, sebbene occupi meno memoria, conserva delle regole e non dei numeri, per cui eseguire calcoli complessi come il calcolo di una inversa, può richiedere maggior tempo rispetto alla equivalente forma completa. Comunque vi sono esempi in cui il calcolo con le matrici sparse risulta vantaggioso anche rispetto ai tempi di elaborazione.
Se si deve costruire una matrice sparsa con elementi non nulli disposti su posizione non esprimibili in maniera diretta tramite un'unica regola, allora si può utilizzare una regola per ciascun elemento o una regola per quegli elementi che rientrano in un determinato criterio e delle singole regole per gli altri.
![]()
![]()
![]()

Costruzione di una matrice con elementi non nulli sulla diagonale principale ed un altro elemento non nullo nella posizione (2,5).
![]()
![]()
![]()
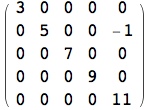
L'esempio che segue mostra come costruire una matrice tridiagonale, tralasciando l’approfondimento della forma delle regole indicate (/; pattern test e :→ rule delayed).
![]()
![]()
![]()

Si costruiscono due matrici triangolari, superiore ed inferiore, rispettivamente:
![]()
![]()
![]()

![]()
![]()
![]()

Come ultimo esempio sulle matrici sparse, si riporta un ulteriore caso in cui la forma sparsa introdotta con SparseArray permette ora di eseguire calcoli praticamente impossibili con la equivalente forma completa. Si costruisce una matrice con ![]() elementi.
elementi.
![]()
![]()
![]()
In questo caso non si può creare la forma completa in quanto non vi è memoria sufficiente sul computer. Si effettueranno solo i calcoli dei byte impiegati da entrambe le forme per verificare la convenienza della forma sparsa. La matrice in forma completa deve memorizzare ![]() ×
×![]() numeri reali generati casualmente con la RandomReal[], ciascuno dei quali richiede 24 byte di memoria (nella versione 8 di Mathematica).
numeri reali generati casualmente con la RandomReal[], ciascuno dei quali richiede 24 byte di memoria (nella versione 8 di Mathematica).
![]()
![]()
![]()
![]()
Pertanto, il numero totale di byte necessari per salvare tutti gli elementi, compresi quelli nulli, è dato dal seguente calcolo:
![]()
![]()
mentre la matrice sparsa occupa soltanto poco più di 40 MegaByte:
![]()
![]()
In questo caso, oltre al vantaggio di ridurre la memoria, si ottiene anche quello di poter eseguire calcoli su matrici così grandi.
Si calcola ora un sistema lineare la cui matrice dei coefficienti è quella creata in precedenza, ed il vettore dei termini noti è creato con ![]() numeri reali casuali. La velocità ottenuta è anche dovuta alla funzione LinearSolve che è in grado di applicare algoritmi ottimizzati per le matrici sparse.
numeri reali casuali. La velocità ottenuta è anche dovuta alla funzione LinearSolve che è in grado di applicare algoritmi ottimizzati per le matrici sparse.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Si è appena risolto un sistema di 1.000.000 equazioni in 1.000.000 di incognite, con una matrice dei coefficienti tridiagonale! In questo caso anche il prodotto di matrici sparse è sorprendentemente veloce:
![]()
![]()
Se si dispone di una matrice in forma completa e la si vuole convertire nella forma sparsa, si può ancora utilizzare SparseArray:
![]()
![]()
![]()
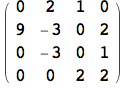
![]()
![]()
![]()

![]()
![]()
Infine, si segnala che mediante SparseArray è anche possibile creare matrici non necessariamente sparse, dove una parte delle entrate è comunque sempre uguale ad un certo valore.
![]()
![]()
![]()
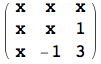
![]()
![]()
![]()
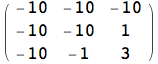
Cenni di programmazione
Mathematica è anche un linguaggio di programmazione. Lo stile di programmazione più vicino alla logica interna di Mathematica è quello funzionale.
Set e SetDelayed
Spesso, quando si assegna un valore ad una variabile di memoria, si parla indifferentemente di assegnazione, definizione o creazione di variabili. In realtà, il vero significato di ciascuna di tali operazioni è la creazione di una regola di sostituzione, che viene poi elaborata dal kernel al momento opportuno, in generale quando la variabile in questione viene riutilizzata in un'espressione successiva alla sua creazione.
Da questo punto di vista Mathematica può essere considerato come un sistema basato esclusivamente sulle regole, in parte definite internamente dal sistema stesso, in parte create dall'utente. Scrivere l'espressione a=0 implica la creazione di una regola che sostituisce tutte le occorrenze del simbolo a con il valore numerico 0. Sebbene, in questo caso, si può dire che il simbolo a assume il significato di variabile di memoria (o brevemente variabile), l'interpretazione dell'operazione a=0 come "la creazione di una regola di sostituzione associata al simbolo a" permette di comprendere meglio la grande differenza tra Mathematica ed altri linguaggi. Infatti, una regola di sostituzione può prevedere l'utilizzo di qualsiasi espressione, non necessariamente un valore numerico.
![]()
![]()
![]()
![]()
![]()
|
![]()
|
In questo caso si è definita una coppia di regole, associate con i simboli a e b; la prima comporta un risultato di tipo numerico, la seconda un risultato di tipo simbolico. Infatti, b=Integrate[Sin[x],x] può essere interpretata come una funzione in quanto il risultato finale, b=-Cos[x], è un'espressione dipendente dalla variabile x, al momento non definita.
![]()
![]()
Questo meccanismo permette di definire funzioni, anche molto complesse, ossia regole di sostituzione che vanno ad aggiungersi a quelle native del sistema.
Per avere una buona padronanza con la creazione e l'utilizzo di regole è opportuno comprendere tre aspetti principali: come viene definita, quando sarà applicata, dove è memorizzata. Il primo aspetto, il modo in cui si definisce una regola, implica gli altri due. Per definire una variabile, ossia associargli una regola di sostituzione, vi sono due istruzioni: Set e SetDelayed. In precedenza si è già visto l'utilizzo dell'operatore usuale Set, indicato con =, per l'assegnazione di un valore o genericamente un'espressione ad una variabile. Si descrive ora un altro operatore di assegnazione molto utilizzato, il SetDelayed, indicato con :=. Si vuole definire una variabile a che assume valori in funzione di un'altra variabile x, mediante una relazione qualsiasi, ad esempio tramite la funzione trigonometrica Sin[x]. Si esegue due volte la stessa operazione, utilizzando i due operatori sopra richiamati.
![]()
![]()
![]()
L'osservazione da fare è che nel primo caso il kernel ha risposto replicando in output la stessa espressione data in input, perché non essendo definito un valore per x la funzione Sin non viene computata; nel secondo caso, invece, non viene restituito alcun output. Da ciò si deduce che, nel primo caso, è stata eseguita una computazione, il cui risultato è Sin[x]. Nel secondo caso, non avendo ottenuto alcun output, si può ipotizzare che il kernel abbia solo registrato la regola indicata, senza effettuare alcuna operazione. In questo esempio le due variabili a e b sono praticamente identiche, come facilmente si verifica:
![]()
![]()
![]()
![]()
![]()
![]()
Anche nel caso in cui si assegni successivamente un valore alla x, le due variabili a e b si comportano allo stesso modo:
![]()
![]()
![]()
![]()
![]()
![]()

| a | b |
| 0.841471 | 0.841471 |
| 0.909297 | 0.909297 |
| 0.14112 | 0.14112 |
| -0.756802 | -0.756802 |
| -0.958924 | -0.958924 |
Qual è, dunque, la differenza tra i due operatori?
In questo esempio non vi sono reali differenze nel modo in cui operano a e b dopo l'assegnazione. Si riporta, allora, un caso analogo, in cui tale differenza viene evidenziata.
Si ripete l'assegnazione di a e b, ora che la variabile x assume un particolare valore.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Sembrerebbe che non vi siano ancora differenze. Si provi ora a cambiare il valore della x:
![]()
![]()
![]()
![]()
![]()
![]()

| a | b |
| 0. | 0.841471 |
| 0. | 0.909297 |
| 0. | 0.14112 |
| 0. | -0.756802 |
| 0. | -0.958924 |
In definitiva, l'operatore Set valuta il suo lato destro immediatamente e memorizza il risultato in a, mentre SetDelayed memorizza il suo lato destro senza valutarlo immediatamente, operazione che verrà eseguita solo successivamente, ogni qual volta verrà chiesto dall'utente di utilizzare la variabile b. In generale, dunque, l'assegnazione di una regola con SetDelayed, non tiene conto del valore delle variabili e dei risultati delle operazioni indicate nella definizione, al momento della sua creazione. Tali elementi avranno il loro effetto solo dopo, quando la regola viene utilizzata.
Per una conferma, basta vedere come il sistema ha memorizzato le due variabili:
![]()
|
![]()
|
Per visualizzare solo le definizioni associate ad un simbolo, si può anche utilizzare la funzione Definition.
![]()
|
![]()
|
Si riportano ancora due esempi che mostrano in maniera più marcata la differenza tra i due operatori di assegnazione sopra visti, evidenziando anche che la loro differenza non dipende solo da eventuali variabili preesistenti, ma anche dalle operazioni specificate a destra dell'operatore di assegnazione.
![]()
![]()
![]()
Le due variabili memorizzano espressioni diverse:
![]()
![]()
Infatti, modificando il valore della x, esse si comportano in maniera differente:
![]()
![]()
![]()
![]()
![]()
![]()

| a | b |
![]()
Altro esempio:
![]()
![]()
![]()
Il valore di a è calcolato in maniera casuale ma solo la prima volta, perché si è utilizzata l'assegnazione immediata, mentre b assume un valore casuale ogni volta che viene richiamata.

| a | b |
| 25 | 26 |
| 25 | 98 |
| 25 | 66 |
| 25 | 86 |
| 25 | 7 |
Definizione di funzioni
La definizione di funzione risulta utile in moltissimi casi, infatti è una delle caratteristiche di Mathematica maggiormente utilizzate.
![]()
![]()
Per utilizzare la funzione così definita, d'ora in poi bisognerà chiamarla passandogli un argomento, altrimenti non vi sarà alcun output:
![]()
![]()
![]()
![]()
![]()
![]()
![]()

| f[x] | |
| -2 | |
| -1 | |
| 0 | 0 |
| 1 | |
| 2 |
La f così definita può essere richiamata con un qualsiasi tipo di argomento, non necessariamente numerico. Questo implica che è possibile usare la definizione di f[x] anche per calcoli simbolici o per visualizzarne il grafico.
![]()
![]()
![]()

![]()

![]()
![]()
Si noti che, avendo utilizzato il SetDelayed, la variabile x che compare nella definizione della funzione non viene a sovrapporsi con eventuali valori della x assegnati in precedenza o che si assegneranno successivamente; in tali casi la variabile assume il senso di variabile locale.
![]()
Viene assegnato un valore alla x:
![]()
![]()
Viene definita la funzione f:
![]()
Il valore di f non dipende dal valore di x definito in precedenza.
![]()
Anche le modifiche di x successive alla definizione di f non ne influenzano il comportamento.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Si noti, però, la differenza nel momento in cui la funzione f viene chiamata passandogli come argomento la variabile x.
![]()
![]()
Infatti, essendo x definita come x=10, prima di eseguire il corpo della funzione f viene valutato il valore di x. Per comprendere meglio come viene elaborato tale input, si può utilizzare la funzione Trace, che mostra i passaggi del kernel nell'applicare tutte le regole definite dall'utente.
![]()
![]()
Dunque, scrivere f[x] equivale a f[10].
Ritornando alla forma usata per definire f, si sarà notato l'uso del trattino di sottolineatura _ (chiamato anche Blank[]) al fianco del nome dell'argomento, nella parte sinistra dell'assegnazione (lhs). Il suo significato è molto articolato e, per il momento, è sufficiente interpretarlo come "il modello o pattern di una qualsiasi espressione accettata da Mathematica". In altre parole nelle definizioni del tipo f[x_]:=CorpoDellaFunzione, esso indica che la funzione f sarà eseguita quando verrà chiamata con un solo argomento (perché c'è un solo parametro x) che può assumere la forma di una qualsiasi espressione sintatticamente corretta. Più in avanti si avrà modo di approfondire tale argomento, che rientra nel meccanismo del pattern matching. È importante ricordarsi che il simbolo _ deve essere utilizzato solo per la definizione della funzione e non quando, successivamente, si usa la funzione stessa.
Il concetto di qualsiasi espressione è molto forte, in quanto davvero è possibile passare qualunque oggetto ad una funzione, come mostrano gli esempi che seguono.
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
Si supponga ora di voler definire la funzione f con tre differenti valori. Una possibilità offerta da Mathematica è quella di utilizzare l'indicizzazione della variabile f come segue:
![]()
![]()
![]()
![]()
In tal modo è possibile far riferimento ad una qualsiasi delle definizioni della funzione f indicando l'indice opportuno. Se, ad esempio, si desidera eseguire il grafico delle tre definizioni si può scrivere:
![]()

Oppure, si potrebbe scegliere a caso una delle tre funzioni e calcolarne il valore in un determinato punto.
![]()
![]()
Come si osserva facilmente, dunque, si ha un'espressione la cui head non è un atomo, bensì ancora un'espressione.
![]()
|
![]()
Si riporta ora un ultimo esempio relativo alla definizione di funzioni per casi particolari. Si vuole definire una funzione ricorsiva. Ad esempio una funzione del tempo che, ad ogni istante, calcola la somma dei valori assunti dalla funzione negli istanti precedenti più un certo valore funzione dell'istante corrente. Si può procedere come segue.
Per effettuare prove su un numero elevato di chiamate ricorsive, si rimuove il limite impostato dalla variabile $RecursionLimit sul numero di chiamate ricorsive.
![]()

![]()
![]()
Si osservi bene cosa accade ad ogni chiamata della funzione R[t]:
![]()

Come si vede con l'aiuto della Trace, il calcolo di ciascun valore di R viene eseguito secondo la formula ricorsiva assegnata. L'effetto poco gradevole di tale metodo è che non vengono memorizzati i valori precedenti di R che potrebbero servire per essere visualizzati o per eventuali chiamate successive della R, senza volerli ricomputare. Per ovviare a questo problema, si potrebbe aggiungere qualche altro comando, ad esempio:
![]()
![]()
![]()
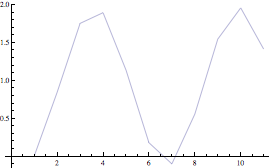
Si sono salvati i valori precedenti nella variabile valori, ma non si è risolto il problema di evitare che essi vengano computati nelle successive chiamate di R[t]. Le due linee di input che seguono mostrano come tra una chiamata e l'altra non vi sia una differenza significative di tempo, in quanto in entrambe vengono ricalcolati tutti i valori di R:
![]()
![]()
![]()
![]()
Esiste un modo più semplice ed efficiente per ottenere il risultato desiderato, cioè memorizzare i valori precedenti in maniera da poterli visualizzare e riutilizzare nei calcoli successivi risparmiando tempo. Si ridefinisce la funzione R nel seguente modo.
![]()
![]()
![]()
|
Si osservi che è possibile indicare la funzione R[t] a sinistra di due assegnazioni nidificate. Nella prima R[t_] definisce la regola generale, mentre nella seconda R[t] memorizza il valore ad ogni chiamata con un t fissato. Si provi a chiedere il calcolo di R[10] e successivamente si osservi cosa è cambiato nella definizione di R:
![]()
![]()
![]()
|
Come anticipato, ad ogni chiamata di R con un t fissato, viene calcolato R[t] e contemporaneamente vengono memorizzati i risultati per tutti i valori di k<t. Per riutilizzare tali valori basta richiamare R[k], con k<t, senza bisogno di salvarli in una variabili di appoggio.
![]()

Altro vantaggio evidente è che, una volta calcolato R[t] per un qualsiasi valore di t, le definizioni di R già note vengono utilizzate anche per il calcolo di R[w] con w>t. La conferma viene data sia dalla Trace che dalla Timing:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Si definisca ora una funzione per il calcolo delle radici n-sime di un numero complesso z:
![]() =
= ![]() (cos(
(cos(![]() ) + i sin(
) + i sin(![]() )) con k = 0,1, ..., n-1, φ argomento di z e ρ modulo di z.
)) con k = 0,1, ..., n-1, φ argomento di z e ρ modulo di z.
Bisogna creare una funzione che richiede in input due argomenti, il numero complesso e l'indice della radice. Tutto quello che bisogna fare è specificare la sua forma nella parte a sinistra dell'operatore := e l'algoritmo per il calcolo nella parte destra dell'operatore, come nella seguente espressione.
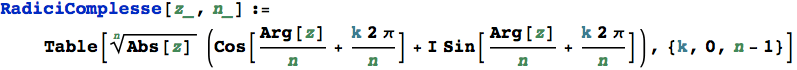
![]()
![]()
Come ultima osservazione, si noti che anche per le funzioni definite dall'utente si ha disposizione il meccanismo del completamento automatico del nome e dell'espressione. Per quanto riguarda il primo, è immediatamente disponibile non appena si è definita la funzione. Infatti, si provi a digitare solo le prime tre lettere del nome RadiciComplesse, e poi si digiti [CTRL] -[k]. Apparirà la finestra che indica tutte le funzioni il cui nome comincia con Rad, come in figura:

Per quanto riguarda, invece, il completamento automatico dell'espressione, bisogna definire un ulteriore elemento per la funzione RadiciComplesse, ossia il suo messaggio di help in linea. Per fare ciò si utilizza la seguente espressione:
![]()
![]()
In tal modo si è creato il messaggio di help che compare quando si utilizza il simbolo ?
![]()
e, contemporaneamente, si è creata l'espressione tipo che compare con il completamento automatico dato dalla sequenza [SHIFT]+[CTRL] -[k]. Si provi con la scritta seguente:
![]()
comparirà
![]()
La Grafica
Come per ogni altro oggetto di Mathematica, il grafico ha un significato ed una forma per l’utente, ed un altro significato ed un’altra corrispondente forma per il sistema. A tal proposito è bene distinguere la generazione dell’oggetto grafico (e quindi della sua forma interna) dalla visualizzazione del grafico stesso.
Quindi si possono distinguere due classi di istruzioni per la grafica: quelle che sono in grado di generare un oggetto grafico e di mostrarlo (ad esempio Plot, ParametricPlot, ListPlot, etc.), e quelle che sono in grado semplicemente di generarlo (ad esempio Graphics, Graphics3D, etc.) e che necessitano poi di una funzione di supporto, chiamata Show, per mostrare il grafico.
Grafici 2D di funzioni
Plot e ListPlot
Per effettuare il grafico di una funzione espressa in forma analitica bisogna utilizzare la funzione Plot. Ad esempio, se si vuole visualizzare il grafico della funzione Sin[x], bisogna indicare al sistema sia la funzione, sia l’intervallo da utilizzare sull’asse delle x. Come accennato nel precedente paragrafo, questa informazione è indispensabile al sistema per poter eseguire il grafico, in quanto la funzione seno, essendo definita in R, può essere disegnata da -∞ a + ∞. Dunque, il secondo argomento della Plot sarà una lista del tipo {x, xmin, xmax}.
![]()
![]()
Cosa è cambiato rispetto a prima ?
Manca la cella di output, infatti è stato semplicemente generato il grafico ma non è comparsa alcuna cella con la label Out[n]:=. Il trucco utilizzato è il punto e virgola alla fine della linea di input, che ha l'effetto di inibire la visualizzazione dell'output. La cella contenente il grafico non viene etichettata come cella di output e questo significa che non lo è (se lo fosse stato non sarebbe comparsa a causa del ;). In conclusione, la visualizzazione del grafico può essere considerata come un effetto collaterale (side effect), che eventualmente può anche essere eliminato, e non come un risultato della funzione Plot.
Ritornando alla risposta ottenuta in precedenza, avendo specificato che la variabile indipendente x varia da -π a π, il sistema determina 25 punti equidistanti tra loro, nell'intervallo [-π,π], per i quali calcola il valore dell'immagine Sin[![]() ] effettuando così la discretizzazione della funzione continua Sin[x]. Successivamente, esegue alcuni algoritmi di interpolazione per calcolare ulteriori valori della funzione al di fuori dei 25 già ottenuti al primo passo. A questo punto il sistema dispone degli opportuni elementi per eseguire il grafico. L'oggetto grafico generato ha una head di tipo Graphics seguita da una tabella con coppie ordinate (
] effettuando così la discretizzazione della funzione continua Sin[x]. Successivamente, esegue alcuni algoritmi di interpolazione per calcolare ulteriori valori della funzione al di fuori dei 25 già ottenuti al primo passo. A questo punto il sistema dispone degli opportuni elementi per eseguire il grafico. L'oggetto grafico generato ha una head di tipo Graphics seguita da una tabella con coppie ordinate (![]() , Sin[
, Sin[![]() ]) ed alcune direttive che impostano l'aspetto del grafico. Trattandosi di una Plot, una delle istruzioni che generano e mostrano i grafici, il sistema prosegue automaticamente con la visualizzazione del grafico. Per avere conferma di cosa viene realmente computato quando si chiama la funzione Plot, è sufficiente chiedere la FullForm o la InputForm di uno degli output precedenti:
]) ed alcune direttive che impostano l'aspetto del grafico. Trattandosi di una Plot, una delle istruzioni che generano e mostrano i grafici, il sistema prosegue automaticamente con la visualizzazione del grafico. Per avere conferma di cosa viene realmente computato quando si chiama la funzione Plot, è sufficiente chiedere la FullForm o la InputForm di uno degli output precedenti:
![]()
Grafica 3D
![]()
Analogamente alla grafica bidimensionale, è possibile utilizzare gli stessi comandi nella versione 3D. Ad esempio:
![]()
![]()
E’ anche possibile variare dinamicamente il grafico con la funzione Manipulate.
![]()

![]()
![]()
Graphics[{{{}, {}, {Hue[0.67, 0.6, 0.6], Line[{{-3.1415925253615216, -1.2822827167891634*^-7},
{-3.1396654880578843, -0.001927164339004342}, {-3.137738450754247, -0.003854193293266924},
{-3.1338843761469724, -0.007708201108565661}, {-3.1261762269324227, -0.015415816004009004},
{-3.110759928503324, -0.03082784009467822}, {-3.0799273316451266, -0.061626247826437476},
{-3.0182621379287315, -0.12301810194283713}, {-2.8845578654095836, -0.2542138749185556},
{-2.759713948540342, -0.3726645007390022}, {-2.637318973742252, -0.4831716559080398},
{-2.5045501138578046, -0.5948206667810294}, {-2.3806416096232637, -0.6896104843619676},
{-2.246359220302365, -0.7803550768254575}, {-2.2442993226890877, -0.7816415498416074},
{-2.24223942507581, -0.7829247062145637}, {-2.2381196298492556, -0.7854810472663536},
{-2.2298800393961464, -0.7905536910323365}, {-2.213400858489928, -0.8005376246467046},
{-2.1804424966774913, -0.8198506642936907}, {-2.114525773052618, -0.8557852784294557},
{-2.1126043184963703, -0.8567777264106475}, {-2.1106828639401227, -0.8577670111800606},
{-2.106839954827628, -0.8597360764855386}, {-2.099154136602638, -0.8636360886325236},
{-2.0837825001526578, -0.8712828366943679}, {-2.0530392272526976, -0.885956967864959},
{-2.05111777269645, -0.8868464399329707}, {-2.0491963181402024, -0.8877326377759202},
{-2.0453534090277077, -0.8894951977114103}, {-2.0376675908027178, -0.892980883732507},
{-2.0222959543527375, -0.8997938037956825}, {-1.9915526814527773, -0.9127802676472788},
{-1.9894691349420555, -0.9136293123298868}, {-1.9873855884313336, -0.9144743907973654},
{-1.98321849540989, -0.9161526344296695}, {-1.9748843093670025, -0.9194613668487992},
{-1.9582159372812278, -0.9258870137580499}, {-1.9248791931096783, -0.9379648812640385},
{-1.9227956465989564, -0.9386852734597926}, {-1.9207121000882346, -0.9394015906683685},
{-1.9165450070667909, -0.9408219877030861}, {-1.9082108210239035, -0.9436137462886433},
{-1.8915424489381287, -0.9490004488089845}, {-1.858205704766579, -0.9589814532774428},
{-1.8562606013128868, -0.959531014993981}, {-1.854315497859195, -0.9600769463956867},
{-1.8504252909518106, -0.9611579100063793}, {-1.8426448771370425, -0.9632761834893662},
{-1.8270840495075058, -0.967337671332559}, {-1.8251389460538139, -0.9678289078627276},
{-1.8231938426001217, -0.968316482683598}, {-1.8193036356927377, -0.9692806398324918},
{-1.8115232218779693, -0.9711649333808123}, {-1.7959623942484328, -0.9747570429220562},
{-1.794017290794741, -0.9751894785134672}, {-1.7920721873410488, -0.9756182245474039},
{-1.7881819804336647, -0.9764646414683034}, {-1.7804015666188964, -0.9781131301827486},
{-1.76484073898936, -0.9812323825384774}, {-1.762895635535668, -0.9816055983862322},
{-1.7609505320819758, -0.9819751004015963}, {-1.7570603251745918, -0.9827029573572739},
{-1.7492799113598234, -0.9841140447107248}, {-1.733719083730287, -0.9867574189497462},
{-1.7318122449964566, -0.9870649196839719}, {-1.7299054062626262, -0.9873688314177196},
{-1.7260917287949655, -0.9879658834767021}, {-1.7184643738596443, -0.9891168718422976},
{-1.7165575351258142, -0.989395630363058}, {-1.7146506963919839, -0.9896707914087997},
{-1.7108370189243232, -0.9902103170863328}, {-1.7032096639890018, -0.9912461555962515},
{-1.7013028252551714, -0.9914961070359759}, {-1.699395986521341, -0.9917424533632794},
{-1.6955823090536806, -0.992224327110842}, {-1.6879549541183594, -0.9931447747237425},
{-1.6727002442477168, -0.9948122874129468}, {-1.6707934055138867, -0.9950044569152443},
{-1.6688865667800563, -0.9951930085486456}, {-1.6650728893123956, -0.9955592554795967},
{-1.6574455343770742, -0.9962483056308925}, {-1.6555386956432439, -0.9964115137227522},
{-1.6536318569094135, -0.9965710988296106}, {-1.649818179441753, -0.9968793977804729},
{-1.6421908245064318, -0.9974524952137558}, {-1.6402839857726015, -0.9975867039163834},
{-1.6383771470387711, -0.9977172853609796}, {-1.6345634695711104, -0.9979675645900753},
{-1.63265663083728, -0.9980872614645513}, {-1.6307497921034497, -0.9982033292609522},
{-1.6269361146357892, -0.998424575944621}, {-1.6250292759019591, -0.9985297540274285},
{-1.6231224371681288, -0.9986313014232436}, {-1.619308759700468, -0.9988235026901805},
{-1.6174019209666377, -0.9989141558624522}, {-1.6154950822328074, -0.9990011769500337},
{-1.6116814047651467, -0.9991643216186876}, {-1.609612474076842, -0.9992467479388707},
{-1.6075435433885374, -0.9993248970106624}, {-1.6054746127002328, -0.9993987684995478},
{-1.603405682011928, -0.9994683620893222}, {-1.6013367513236232, -0.9995336774820919},
{-1.5992678206353186, -0.9995947143982763}, {-1.5951299592587094, -0.9997039517741367},
{-1.5930610285704048, -0.999752151766225}, {-1.5909920978821002, -0.9997960723465549},
{-1.5889231671937956, -0.9998357133271253}, {-1.5868542365054907, -0.9998710745382542},
{-1.584785305817186, -0.9999021558285789}, {-1.5827163751288813, -0.9999289570650568},
{-1.5806474444405767, -0.9999514781329658}, {-1.578578513752272, -0.9999697189359052},
{-1.5765095830639675, -0.9999836793957958}, {-1.5744406523756629, -0.9999933594528801},
{-1.5723717216873583, -0.9999987590657231}, {-1.5703027909990535, -0.9999998782112116},
{-1.5682338603107486, -0.9999967168845553}, {-1.566164929622444, -0.9999892750992861},
{-1.5640959989341394, -0.9999775528872585}, {-1.5620270682458348, -0.999961550298649},
{-1.5599581375575302, -0.9999412674019562}, {-1.5578892068692256, -0.9999167042840006},
{-1.555820276180921, -0.9998878610499239}, {-1.5537513454926162, -0.9998547378231887},
{-1.5516824148043113, -0.9998173347455782}, {-1.5496134841160067, -0.9997756519771952},
{-1.5475445534277021, -0.9997296896964616}, {-1.5454756227393975, -0.9996794481001178},
{-1.543406692051093, -0.9996249274032214}, {-1.5413377613627883, -0.9995661278391469},
{-1.5392688306744837, -0.9995030496595843}, {-1.537199899986179, -0.9994356931345377},
{-1.535130969297874, -0.9993640585523252}, {-1.5330620386095695, -0.9992881462195765},
{-1.5289241772329603, -0.9991234896205429}, {-1.5268552465446557, -0.9990347460590658},
{-1.524786315856351, -0.9989417261566659}, {-1.5206484544797416, -0.9987428589400764},
{-1.512372731726523, -0.9982938271614664}, {-1.5103038010382184, -0.9981708850461835},
{-1.5082348703499138, -0.9980436702877108}, {-1.5040970089733043, -0.9977764250376406},
{-1.4958212862200857, -0.9971906880040196}, {-1.493752355531781, -0.9970335810141969},
{-1.4916834248434765, -0.9968722062493834}, {-1.4875455634668673, -0.9965366561760906},
{-1.4792698407136486, -0.9958143743466596}, {-1.4773393530823737, -0.9956360747050302},
{-1.475408865451099, -0.9954540645454591}, {-1.4715478901885493, -0.9950789153995656},
{-1.4638259396634496, -0.9942841216643886}, {-1.4618954520321747, -0.9940761576460223},
{-1.4599649644008998, -0.9938644889231839}, {-1.4561039891383503, -0.9934300405332672},
{-1.4483820386132509, -0.9925167229335421}, {-1.446451550981976, -0.9922791441397993},
{-1.444521063350701, -0.992037867338661}, {-1.4406600880881513, -0.9915442233247194},
{-1.4329381375630519, -0.990512599695223}, {-1.417494236512853, -0.98827222995154},
{-1.415563748881578, -0.9879755986512128}, {-1.413633261250303, -0.9876752853818631},
{-1.4097722859877533, -0.9870636174266213}, {-1.402050335462654, -0.9857961480515995},
{-1.386606434412455, -0.9830849445640588}, {-1.355718632312057, -0.976959815340046},
{-1.3536260527263078, -0.9765110713568594}, {-1.3515334731405586, -0.9760580513413295},
{-1.34734831396906, -0.9751391911668499}, {-1.3389779956260632, -0.9732502469670654},
{-1.3222373589400696, -0.9692679326365599}, {-1.2887560855680822, -0.9604896062780457},
{-1.286663505982333, -0.9599051056843635}, {-1.2845709263965839, -0.9593164017739971},
{-1.2803857672250853, -0.9581263943330793}, {-1.2720154488820885, -0.9556960543090358},
{-1.2552748121960948, -0.9506346758110857}, {-1.2217935388241077, -0.9397141875380658},
{-1.21973922395822, -0.9390097098112608}, {-1.2176849090923327, -0.9383012692680874},
{-1.213576279360558, -0.9368725117084131}, {-1.205359019897008, -0.9339675754613148},
{-1.1889245009699083, -0.9279687105727976}, {-1.1560554631157087, -0.9152207709228336},
{-1.09031738740731, -0.886773656821457}, {-1.0884015155984523, -0.8858865063862249},
{-1.0864856437895947, -0.884996104248171}, {-1.0826539001718793, -0.8832055579486322},
{-1.0749904129364487, -0.8795855895181174}, {-1.0596634384655872, -0.8721908974026384},
{-1.0290094895238644, -0.8567886352600308}, {-0.9677015916404187, -0.8235842465112403},
{-0.9656236278770867, -0.822403860772279}, {-0.9635456641137548, -0.8212199239494953},
{-0.9593897365870907, -0.8188414175164063}, {-0.9510778815337626, -0.8140420176039473},
{-0.9344541714271064, -0.8042748352072092}, {-0.9012067512137942, -0.7840764676698921},
{-0.8347119107871697, -0.7411031219178129}, {-0.7105825855838271, -0.6522754710746895},
{-0.5760793752941268, -0.5447402771484028}, {-0.4440251070755782, -0.42957772713203446},
{-0.3208311945069359, -0.31535545112602165}, {-0.18726339685193602, -0.18617083526814404},
{-0.06255595484684248, -0.06251516334017546}, {0.05970254508709937, 0.05966708417636896},
{0.1923349301073989, 0.19115128932767714}, {0.3161069594777921, 0.31086877425751963},
{0.45025287393454294, 0.43519321980343845}, {0.5819498463201421, 0.5496538676123238},
{0.7047864630558349, 0.6478711825589072}, {0.8379969648778853, 0.7433046755726653},
{0.8399399359118251, 0.744603028081636}, {0.8418829069457648, 0.7458985696134673},
{0.8457688490136444, 0.748481200192964}, {0.8535407331494034, 0.7536125151423861},
{0.8690845014209213, 0.7637382790138121}, {0.9001720379639573, 0.7834338385481855},
{0.9623471110500293, 0.8205354257281972}, {0.9642518173641073, 0.8216226585479444},
{0.9661565236781853, 0.8227069105987027}, {0.9699659363063413, 0.8248664566698269},
{0.9775847615626534, 0.8291496072337015}, {0.9928224120752775, 0.8375712755391336},
{1.0232977131005256, 0.8538292962794414}, {1.0252024194146037, 0.8548192476558032},
{1.0271071257286817, 0.8558060978291029}, {1.0309165383568377, 0.8577704802569853},
{1.0385353636131498, 0.861661873902664}, {1.0537730141257737, 0.8692943895789494},
{1.0842483151510218, 0.8839521934370741}, {1.086315113419574, 0.8849166927083625},
{1.0883819116881264, 0.8858774119221082}, {1.0925155082252311, 0.8877874937776974},
{1.1007827012994404, 0.8915621173125439}, {1.1173170874478593, 0.8989283062064907},
{1.1503858597446968, 0.9129214911665808}, {1.152452658013249, 0.9137630738725806},
{1.1545194562818015, 0.9146007532992909}, {1.1586530528189063, 0.916264388018426},
{1.1669202458931156, 0.9195446617800591}, {1.1834546320415344, 0.9259164475524855},
{1.216523404338372, 0.9378989661064423}, {1.2184517595498945, 0.9385661847535484},
{1.2203801147614168, 0.9392299132928624}, {1.224236825184462, 0.9405468901886646},
{1.2319502460305523, 0.9431388549606083}, {1.2473770877227328, 0.9481542930602083},
{1.2782307711070937, 0.957507096344665}, {1.2801591263186163, 0.958061472095784},
{1.2820874815301386, 0.9586122852448582}, {1.2859441919531838, 0.9597032155572174},
{1.293657612799274, 0.9618422357239118}, {1.3090844544914546, 0.9659484732670754},
{1.3399381378758155, 0.9734703886979993}, {1.3420285850418123, 0.9739465828809344},
{1.3441190322078094, 0.9744185209487}, {1.348299926539803, 0.9753496205079141},
{1.3566617152037908, 0.9771606567479661}, {1.3733852925317658, 0.9805776407913964},
{1.3754757396977628, 0.9809855000855562}, {1.3775661868637596, 0.9813890725047052},
{1.3817470811957535, 0.982183349682318}, {1.390108869859741, 0.9837203851951678},
{1.4068324471877163, 0.9865880110231745}, {1.408922894353713, 0.9869270791939445},
{1.41101334151971, 0.9872618345251944}, {1.4151942358517038, 0.987918400836508},
{1.4235560245156913, 0.9891797162821414}, {1.4256464716816883, 0.989484241832617},
{1.4277369188476852, 0.9897844433688542}, {1.431917813179679, 0.9903718691700314},
{1.4402796018436665, 0.9914947761459183}, {1.4423700490096634, 0.9917646739089757},
{1.4444604961756604, 0.9920302376923802}, {1.448641390507654, 0.9925483586971542},
{1.4570031791716418, 0.9935325431581932}, {1.4737267564996168, 0.9952924474135677},
{1.475678760608584, 0.995479733879968}, {1.477630764717551, 0.9956632272511919},
{1.4815347729354853, 0.9960188319258931}, {1.4893427893713538, 0.9966844943384429},
{1.491294793480321, 0.9968414172764121}, {1.493246797589288, 0.996994541930757},
{1.4971508058072223, 0.9972893940692338}, {1.5049588222430905, 0.9978334942406683},
{1.5069108263520574, 0.9979600153836806}, {1.5088628304610245, 0.9980827339808532},
{1.5127668386789588, 0.9983167616817821}, {1.514718842787926, 0.998428069893818},
{1.516670846896893, 0.9985355737765774}, {1.5205748551148273, 0.9987391669302671},
{1.5225268592237944, 0.9988352554254427}, {1.5244788633327615, 0.9989275380398348},
{1.5283828715506957, 0.9991006842342673}, {1.5303348756596629, 0.9991815471545654},
{1.53228687976863, 0.9992586028745983}, {1.5361908879865642, 0.9994012915539486},
{1.5381428920955313, 0.9994669239695766}, {1.5400948962044985, 0.9995287480975628},
{1.5420469003134656, 0.9995867637023373}, {1.5439989044224327, 0.9996409705628424},
{1.5459509085313998, 0.9996913684725326}, {1.547902912640367, 0.9997379572393758},
{1.549854916749334, 0.9997807366858539}, {1.5518069208583012, 0.9998197066489635},
{1.5537589249672683, 0.9998548669802167}, {1.5557109290762354, 0.9998862175456416},
{1.5576629331852025, 0.9999137582257822}, {1.5596149372941697, 0.9999374889157},
{1.5615669414031368, 0.9999574095249734}, {1.563518945512104, 0.9999735199776986},
{1.565470949621071, 0.9999858202124894}, {1.5674229537300381, 0.9999943101824783},
{1.5693749578390053, 0.9999989898553157}, {1.5713269619479724, 0.9999998592131705},
{1.5732789660569395, 0.9999969182527302}, {1.5752309701659066, 0.9999901669852007},
{1.5771829742748738, 0.9999796054363067}, {1.5791349783838409, 0.9999652336462909},
{1.581086982492808, 0.9999470516699144}, {1.5830389866017751, 0.9999250595764564},
{1.5849909907107422, 0.9998992574497138}, {1.5869429948197094, 0.9998696453880008},
{1.5888949989286765, 0.999836223504149}, {1.5908470030376436, 0.9997989919255063},
{1.5927990071466107, 0.9997579507939368}, {1.5947510112555778, 0.9997131002658205},
{1.5986550194735119, 0.9996119717180407}, {1.6005687588626172, 0.9995568338809568},
{1.6024824982517227, 0.9994980352695916}, {1.6063099770299334, 0.9993694565987994},
{1.6082237164190387, 0.9992996770102787}, {1.610137455808144, 0.9992262375892873},
{1.6139649345863547, 0.9990683803391528}, {1.61587867397546, 0.9989839630881456},
{1.6177924133645654, 0.9988958871609378}, {1.6216198921427762, 0.9987087605815942},
{1.6292748496991978, 0.9982906183991545}, {1.631188589088303, 0.9981769415206927},
{1.6331023284774084, 0.9980596089216638}, {1.636929807255619, 0.9978139782941662},
{1.6445847648120406, 0.9972788681968288}, {1.646498504201146, 0.9971359583355134},
{1.6484122435902515, 0.996989396566125}, {1.6522397223684622, 0.9966853194635713},
{1.6598946799248835, 0.9960333668752154}, {1.6618084193139888, 0.9958612575275348},
{1.6637221587030941, 0.9956855009402421}, {1.6675496374813048, 0.9953230486349368},
{1.6752045950377263, 0.9945544063660271}, {1.6771183344268317, 0.9943531378725059},
{1.6790320738159372, 0.9941482276627058}, {1.6828595525941479, 0.9937274851094543},
{1.6905145101505692, 0.992842333321224}, {1.6924282495396745, 0.9926119528569675},
{1.6943419889287799, 0.9923779370533434}, {1.6981694677069907, 0.9918990028695392},
{1.7058244252634123, 0.990897549031762}, {1.7211343403762551, 0.9887205093335352},
{1.7232101717198347, 0.9884074771998993}, {1.7252860030634145, 0.9880901859450848},
{1.7294376657505741, 0.9874428315591935}, {1.7377409911248929, 0.986097074720369},
{1.7543476418735304, 0.9832016996684039}, {1.7564234732171102, 0.982820695926796},
{1.7584993045606898, 0.9824354571378646}, {1.7626509672478492, 0.9816522810763642},
{1.770954292622168, 0.9800351826482797}, {1.7875609433708055, 0.97659839690468},
{1.7896367747143853, 0.9761498418106065}, {1.791712606057965, 0.9756970804144153},
{1.7958642687451243, 0.9747789465377258}, {1.804167594119443, 0.9728922902155132},
{1.8207742448680808, 0.9689178846305401}, {1.8539875463653561, 0.9601686346199426},
{1.855924934651906, 0.9596254856638148}, {1.8578623229384559, 0.9590787347801052},
{1.8617370995115556, 0.9579744354523099}, {1.8694866526577554, 0.9557227048680358},
{1.8849857589501546, 0.9510471938096914}, {1.9159839715349534, 0.9410119752114038},
{1.9179213598215035, 0.9403546492016029}, {1.9198587481080533, 0.9396937935967694},
{1.923733524681153, 0.9383615035372552}, {1.9314830778273526, 0.935654678306454},
{1.946982184119752, 0.9300726207859763}, {1.9779803967045506, 0.9182396411990777},
{1.9800798769455747, 0.9174061710059198}, {1.982179357186599, 0.9165686570554714},
{1.9863783176686476, 0.9148815126669404}, {1.9947762386327446, 0.9114588624253174},
{2.0115720805609385, 0.9044209668719689}, {2.045163764417327, 0.8895818387807395},
{2.112347132130103, 0.8569103254512642}, {2.1144083476512656, 0.8558460203515084},
{2.116469563172428, 0.8547780790975716}, {2.1205919942147533, 0.85263130629164},
{2.128836856299403, 0.8482943275018884}, {2.145326580468703, 0.8394476742174778},
{2.1783060288073033, 0.8210720854972544}, {2.2442649254845035, 0.7816630038752213},
{2.3673223631889977, 0.6991945692154096}, {2.5007536859798494, 0.5978681634714227},
{2.6253246531207948, 0.4936379843655188}, {2.7474466781905886, 0.38401978680018956},
{2.87994258834674, 0.2586748077042026}, {3.003578142852985, 0.13757677765619036},
{3.005734617579681, 0.13544049038323683}, {3.0078910923063766, 0.1333035732603404},
{3.0122040417597686, 0.1290278892175184}, {3.0208299406665517, 0.12046940037222416},
{3.038081738480119, 0.10332616932911709}, {3.072585334107253, 0.06895256359569414},
{3.074741808833949, 0.06680106274857178}, {3.076898283560645, 0.06464925125102673},
{3.0812112330140367, 0.060344736333044165}, {3.08983713192082, 0.051732419079820444},
{3.1070889297343873, 0.03449687810901539}, {3.1092454044610833, 0.03234160836265002},
{3.1114018791877793, 0.030186188215469225}, {3.115714828641171, 0.02587493681341806},
{3.1243407275479544, 0.017251070275795522}, {3.1264972022746504, 0.015094878014924758},
{3.1286536770013464, 0.012938615557113363}, {3.132966626454738, 0.00862592016072063},
{3.135123101181434, 0.006469507277817497}, {3.1372795759081296, 0.004313064309238206},
{3.1394360506348256, 0.002156601283264238}, {3.1415925253615216,
1.2822827167891634*^-7}}]}}}, {AspectRatio -> GoldenRatio^(-1), Axes -> True,
AxesOrigin -> {0, 0}, PlotRange -> {{-Pi, Pi}, {-0.9999998782112116, 0.9999998592131705}},
PlotRangeClipping -> True, PlotRangePadding -> {Scaled[0.02], Scaled[0.02]}}]
Essendo l'oggetto Graphics una normale espressione di Mathematica, i grafici possono essere manipolati esattamente come tutte le altre espressioni. Tra le altre cose, essi possono essere salvati in una variabile per poi essere rivisualizzati all'occorrenza, ad esempio qualora si vogliano generare più grafici e poi mostrarli contemporaneamente su di uno stesso piano cartesiano. In tale caso si può procedere come segue.
![]()
![]()
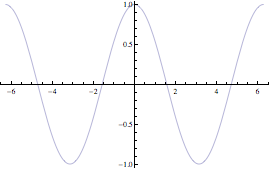
![]()

Nel caso in cui si conoscano le espressioni analitiche di più funzioni, si può richiederne il grafico su di un unico piano cartesiano senza dover prima generare i singoli grafici separatamente e poi unirli con la Show.
![]()
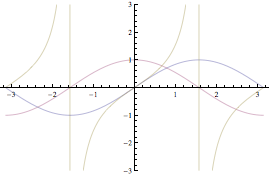
![]()
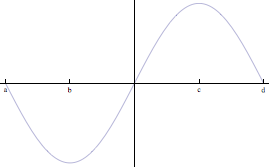
Nel caso precedente, ad esempio, si può inserire un colore nello sfondo del grafico, mediante il comando Show e l' uso dell' opzione Background -> DirettivaColore.
![]()
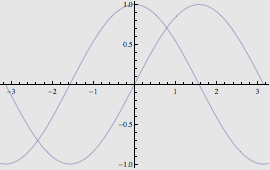
Fino ad ora si è visto come realizzare grafici di funzioni di cui siano note le espressioni analitiche, ma non sempre queste ultime sono disponibili; nella pratica capita spesso di conoscere solo una sequenza di punti, ossia coppie ordinate ![]() , e si ha l'esigenza di conoscere l'andamento di una ipotetica funzione che può assumere quei valori. In questi casi non si può utilizzare la Plot per eseguire il grafico, ma si ha a disposizione un'altra funzione, la ListPlot, che permette di visualizzare nel piano cartesiano i punti assegnati.
, e si ha l'esigenza di conoscere l'andamento di una ipotetica funzione che può assumere quei valori. In questi casi non si può utilizzare la Plot per eseguire il grafico, ma si ha a disposizione un'altra funzione, la ListPlot, che permette di visualizzare nel piano cartesiano i punti assegnati.
Si supponga di avere a disposizione la tabella seguente con 20 coppie ordinate:
![]()
Si richiede al sistema di disegnare tali punti sul piano cartesiano utilizzando la ListPlot:
![]()
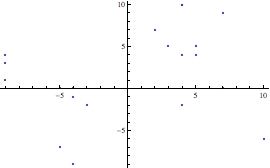
Osservando bene il grafico si comprende che alcuni punti possono risultare difficilmente visibili, soprattutto quelli che hanno una coordinata nulla e quindi giacciono su un asse oppure quelli che capitano dove compaiono i numeri sugli assi. L'esempio seguente evidenzia maggiormente tale problema, ed introduce l'uso delle opzioni per le funzioni grafiche, utili a modificare l'aspetto dei grafici per una loro migliore comprensione.
![]()
![]()
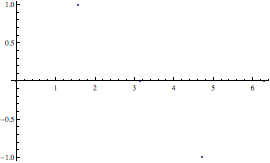
Risulta che solo due punti su cinque, sono visibili. Se si desidera un grafico maggiormente esplicativo, magari con i punti più grandi o di un determinato colore, o magari vedere una linea che li congiunge, si deve operare con le opzioni.
Dunque, per rendere il grafico più esplicito si può, ad esempio, tracciare una linea di colore rosso che congiunge i punti utilizzando le seguenti opzioni:
![]()
![]()
![]()
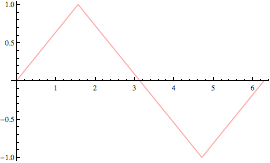
oppure aumentare la dimensione dei singoli punti, in maniera da renderli più visibili:
![]()

Come fare se si desidera impostare contemporaneamente il colore rosso e la taglia per i singoli punti? Con una lista di opzioni:
![]()
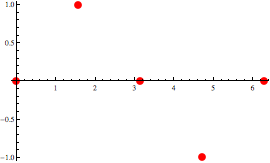
Approfondimenti su alcune opzioni della funzione Plot
AspectRatio
AspectRatio indica il rapporto tra l'altezza e la larghezza del grafico.
![]()

![]()
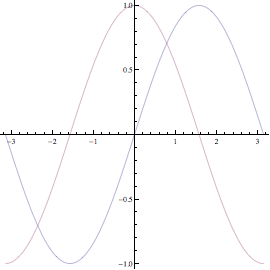
![]()
![]()
PlotRange
Si può specificare qual è l'intervallo desiderato per la y tramite l'opzione PlotRange.
Per vedere solo i valori positivi della funzione Sin[x]:
![]()
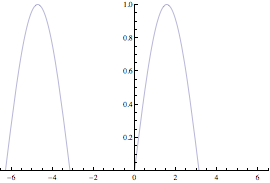
Per vedere solo i valori compresi nell'intervallo [-0.5,0.5]:
![]()
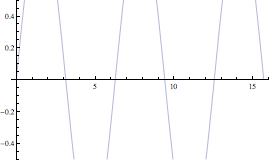
![]()
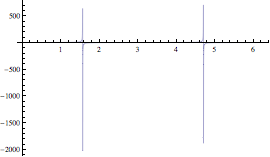
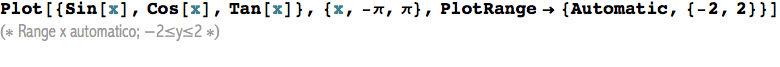
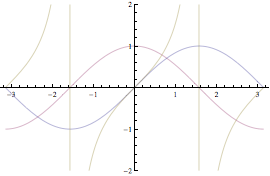
PlotStyle
![]()

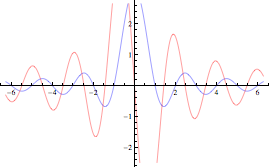
In questo esempio la prima sottolista contiene le direttive per la prima curva (spessore), la seconda quelle per la seconda curva (colore rosso).
![]()
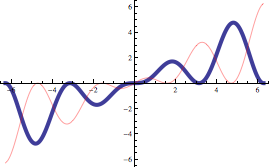
Si supponga, invece, di voler eseguire il grafico con una serie di direttive di stile da applicare ugualmente ad entrambe le funzioni, ad esempio colore rosso (RGBColor[1,0,0]) e spessore 0.01 (Thickness[0.01]). L’espressione è (attenzione alle doppie parentesi graffe):
![]()

Addirittura, volendo indicare alcune direttive solo per una curva si può utilizzare anche la seguente espressione:
![]()
![]()

Ovviamente, quanto sopra detto non è necessario nel caso di un grafico di una sola funzione, per la quale possono essere impartite direttive di stile in un’unica lista di argomenti della PlotStyle.
![]()
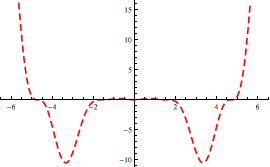
PlotLabel e PlotLegend
Se si desidera aggiungere un titolo al grafico si può utilizzare l'opzione PlotLabel, che aggiunge un'etichetta al riquadro del grafico. Il grafico seguente mostra 3 funzioni disegnate con tre tonalità diverse di grigio ed un titolo che riporta le espressioni delle funzioni stesse.

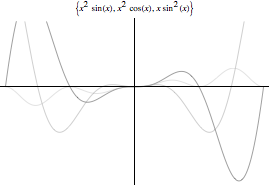
L'opzione PlotLabel non è molto flessibile, in quanto non permette di spostare la posizione della label o di indicare diverse stringhe di testo a seconda delle varie funzioni presenti in un grafico. Una evoluzione della PlotLabel viene fornita dalla PlotLegend, implementata nel pacchetto aggiuntivo PlotLegends. Si mostrano di seguito alcuni esempi.
![]()

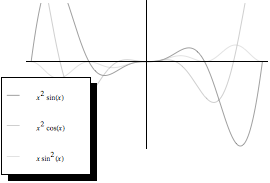
La legenda può essere spostata e modificata mediante l'uso di specifiche opzioni, quali LegendPosition, LegendSize, LegendShadow, LegendOrientation, LegendLabel, LegendBorder, LegendBackground.

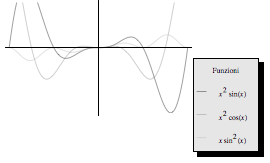
PlotPoints, MaxRecursion
La PlotPoints permette di indicare alla Plot quanti punti campione devono essere presi nell'intervallo specificato per la variabile indipendente. L'opzione PlotPoints interviene sul numero di punti campione e dunque determina una maggiore o minore precisione del grafico. Il valore di default della PlotPoints è 25, ed alcune volte può capitare che con soli 25 punti l'algoritmo di interpolazione restituisca valori eccessivamente approssimati della funzione. In tali casi è possibile chiedere una maggiore precisione, aumentando il numero dei punti campione, mediante la PlotPoints. Nel seguente esempio il calcolo dei punti interpolanti evidentemente comporta un errore di approssimazione in un intorno di x=-60.
![]()
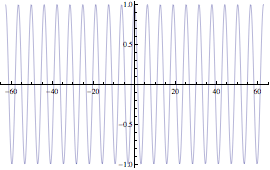
Ovviamente, se si cambia il Range di osservazione, l'errore scompare mostrando il vero comportamento della funzione per x∈{-60,-50}.
![]()
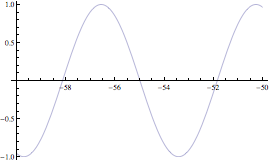
In generale, prima di affidarsi completamente a valutazioni sulla funzione in base al grafico ottenuto, bisogna sempre tenere presente possibili approssimazioni dovute alla visualizzazione del grafico. Seguono alcuni esempi.
![]()
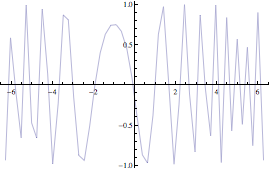
![]()

Filling
![]()