Università di Foggia

Dipartimento di Scienze Biomediche

Prof. Crescenzio Gallo

c.gallo@unifg.it

Reti neurali artificiali con Mathematica

Guerre di Robot!

Lezione 8

Introduzione

Basta con i problemi-giocattolo, iniziamo i combattimenti dei robot! Progetteremo un robot cerca-luce simile al semplice robot che abbiamo proposto in precedenza: solo che in questo caso gli forniremo un controllo un po' più sofisticato. Infine, dopo l'addestramento costruiremo un piccolo campo per testare la rete risultante.

Package

Nel materiale didattico c'è un file chiamato Lezione_07.m (un package Mathematica) che può essere letto con il comando Get:

Ora abbiamo nuovamente a disposizione il set di routine definite nella Lezione 7. Controlliamole usando le query di Mathematica:

Global`setupNN

Global`trainNN

Global`feedForward

Utilizzeremo queste routine, senza modificarle, per la simulazione del nostro mezzo robotizzato.

Il robot fotosensibile

Torniamo indietro al nostro primo capitolo e ricordiamo il robot fotosensibile:

Figura 1. Il robot fotosensibile. Due sensori di luce (analoghi dei neuroni sensoriali) sono montati nella parte anteriore e sono collegati alle ruote motorizzate. In questa semplice configurazione ciascun sensore è collegato direttamente al motore dietro di esso.

Per questo esperimento vogliamo costruire un sistema più sofisticato che potrebbe essere addestrabile o adattabile ad una varietà di circostanze. Per esempio, cosa succede se il robot sopra illustrato deve attraversare una porta o qualche altro passaggio? Che dire della ricerca di altri robot (utilizzando alcuni altri sensori, per esempio, emettitori chimici e ricevitori)?

Esamineremo questi ed altri comportamenti con il nostro robot modificato.

Dettagli progettuali

Ecco una semplice estensione del nostro progetto precedente. Abbiamo mantenuto le stesse ruote motorizzate. Se i motori ricevono un segnale 'positivo' spingono il robot in avanti, un segnale 'negativo' fa spostare all'indietro il robot. Si noti che le ruote rispondono anche in modo proporzionale alla grandezza del segnale; cioè, maggiore è l'ampiezza del segnale, più velocemente i motori girano in qualsiasi direzione. L'ingresso è attualmente composto da sette sensori. Come per i motori, si suppone che anch'essi restituiscano un segnale proporzionale alla quantità totale di luce che influisce su di essi.

Infine, abbiamo lo strato etichettato 'processore'.

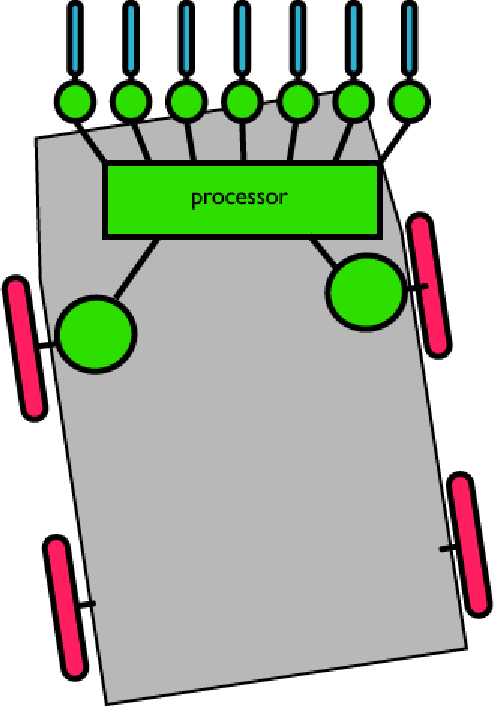
Figura 2. Il progetto migliorato. Abbiamo praticamente aggiunto uno strato 'processore' che, in questo caso, equivale ad uno strato di neuroni artificiali nascosti.

Se si oservano le componenti in verde nella figura del robot si può iniziare a vedere la rete artificiale. La nostra rete avrà sette ingressi (nell'intervallo [0,1], da 0=nessuna luce sino ad 1=massima luce), due uscite (i cui valori dovranno essere trasformati per trovarsi nell'intervallo [-1,1] e rappresentare il movimento, con -1='indietro', 1='avanti' e 0='stop'), e un certo numero di unità nascoste.

Le unità di input sono molto semplici, una unità di ingresso per sensore. Le unità nascoste sono un po' più ambigue. Quante unità nascoste dovremmo avere? Ci sono innumerevoli teorie su questo punto. La risposta più semplice è che si tratta di una questione piuttosto empirica. Si ha solo bisogno di provarlo. In generale, per iniziare è possibile utilizzare per le unità nascoste lo stesso numero di  unità di input. Alcune reti necessitano di più unità (a volte alcuni multipli delle unità di ingresso!) e ad alcune possono bastarne poche. Ancora una volta, una regola empirica è che ci sono probabilmente almeno altrettante unità nascoste quante sono le unità di output, e di solito ce ne saranno almeno quante sono le unità di input. Per il primo addestramento del nostro robot, partiremo con dieci unità nascoste.

Infine, dobbiamo impostare la mappatura dei valori di uscita. In tutti gli esempi precedenti abbiamo utilizzato una funzione  non lineare per modificare l'output dei nostri neuroni chiamata . Il grafico è di questo tipo:

Si noti che, indipendentemente dalle dimensioni dei valori di ingresso, sembra che l'intervallo di valori di uscita sia [0,1]. Ed in effetti, ai fini pratici, l'uscita di questa funzione si trova nell'intervallo (0,1). È per questo che tendiamo ad usare valori come 0.1 e 0.9 per rappresentare gli estremi di ingresso al posto di 0 e 1: la non linearità attraverso la quale passiamo i pesi non raggiungerà mai i limiti 0 e 1.

Vogliamo che le uscite dei motori siano nell'intervallo [-1,1]: ciò significa che abbiamo bisogno di fare un qualche tipo di trasformazione dei valori in quanto la rete opera con valori nell'intervallo [0,1] (basta sottrarre 0.5 e moltiplicare per 2 per passare dalla rappresentazione della rete a quella del motore; inoltre, dividendo l'ingresso del motore per 2 e aggiungendo 0.5 si ottiene la trasformazione contraria). Queste operazioni entreranno in gioco quando faremo l'addestramento ed il test del modello.

Addestramento

Per iniziare abbiamo bisogno di creare un training set. Ci sono sette ingressi alla nostra rete artificiale: ciò significa che, se ogni ingresso fosse binario (on/off) avremmo modelli di input possibili. Ci piacerebbe farla franca con un numero significativamente minore di set e vedere se la rete si può generalizzare da loro. Vale a dire, dopo tutto, una delle cose interessanti sulle reti neurali: la loro capacità di riconoscere i modelli che non hanno mai visto prima e classificarli correttamente.

Così, forniremo alla rete alcuni pattern e comportamenti dei motori. Manterremo semplice l'attivazione dei sensori di input per l'addestramento, un sistema 'tutto o niente' in cui il sensore rileva la luce oppure no. Per il controllo del motore proveremo con tre stati discreti － avanti veloce (fast), avanti lento (slow) oppure stop. Ci piacerebbe che il nostro robot cercasse la luce cioè, quando rileva la luce, dovrebbe indirizzarsi verso di essa. Per ora, il robot funzionerà solo muovendo i motori in avanti.

La prima voce del nostro training set ha due sensori che rilevano la luce sul lato estremo sinistro della matrice di sensori. Per orientarsi verso quella luce che dovrebbe fare avanzare la ruota destra e fermare la sinistra. Si noti che la velocità di avanzamento è mappata a 0.9 e la velocità di arresto viene mappata a 0.1; 'avanti lento' è a metà strada a 0.5. Come abbiamo sottolineato in precedenza, per il modo in cui abbiamo impostato la rete possiamo solo usare i numeri nell'intervallo [0,1] per il training della rete. Saremo in grado di 'annullare' questa trasformazione come descritto in precedenza quando l'addestramento sarà concluso.

Quindi, usiamo la routine setupNN per generare le matrici dei pesi per la nostra rete. Questa versione della routine ha come argmenti la dimensione dello strato di input, dello strato nascosto e dei vettori di output.

OK: siamo pronti ad addestrare la nostra rete! Diamole fino a 5000 iterazioni ed osserviamo gli errori per vedere se dobbiamo andare oltre:

Quanto ci ha messo in realtà?

Meno di 5000 iterazioni.

Molto bene. Si noti che il tasso di errore complessivo è sceso al di sotto di 1 decimale. Facciamo passare il nostro training set attraverso la rete per vedere se si comporta bene per quello che vogliamo che 'apprenda':

Rispetto al training set:

i risultati sono sicuramente abbastanza vicini da poter utilizzare la rete per il test. Presentiamo alla rete un paio di input non ancora esaminati. Questo simula la capacità di generalizzazione del robot.

Il tutto sembra avere senso. Quando c'è una luce giusto davanti al robot tutte le unità sono in movimento con un valore > 0.5 (0.5 rappresenta il movimento 'avanti lento') e sembra che ci sia proporzionalmente più velocità sulle ruote lontane dalla luce. Si noti l'ultimo caso, dove non c'è luce. In questo caso il robot procede, anche se lentamente, in avanti (e in questo caso, leggermente verso sinistra, con il motore destro che gira più veloce di quello sinistro).

Salviamo lo stato in modo che possiamo caricare questo robot all'occorrenza senza la necessità di ri-addestrarlo ogni volta.

Da esplorare

Manipolare il numero di unità nascoste. Qual è il minor numero con il robot che impara ancora dal training set originale?

Manipolare il training set. Aggiungere alcuni input. Aggiungere anche del 'rumore'. La rete è ancora in grado di fare un buon lavoro?

Aggiungere un caso speciale per quando non ci sono luci visibili. Vogliamo che il robot giri intorno lentamente finché non si dirige verso una luce. Addestrare la rete e quindi verificare questo scenario.

Testare il modello con valori diversi da 'on' e 'off' per i valori dei sensori. Che cosa succede se abbiamo una fonte di luce  obliqua davanti al robot e il sensore non è completamente illuminato?

Scendiamo in campo!

È interessante chiedersi come si comporterebbe il nostro robot esaminando gli output per qualche data configurazione di ingresso della luce. Mettiamo insieme un banco di prova per il nostro robot: l'ARENA!

Per facilitare le cose abbiamo bisogno di fare alcune ipotesi.

In primo luogo, assumiamo un tempo discreto. Questo significa che calcoleremo la posizione del robot ad intervalli discreti ('tick') di tempo. Ad ogni tick, il robot avanzerà in base all'uscita della rete neurale.

In secondo luogo, per la realizzazione dell'arena assumeremo che i sensori siano montati su una sorta di 'torretta' che li mantiene costantemente rivolti in avanti, indipendentemente dall'orientamento del robot al momento. Cioè, man mano che il robot si dirige verso sinistra o verso destra i sensori rimarranno dritti di fronte alla luce. Rimuoveremo questa restrizione in una versione successiva del robot e dell'arena.

Infine, supponiamo una fonte di luce statica, senza disturbo. Ancora una volta, in seguito ci sbarazzeremo di questa ipotesi per rendere le cose più interessanti.

Figura 3. L'arena. Per questa simulazione, ci limiteremo a usare una specie di pista da bowling.

Il controllo direzionale è un po' più interessante. Per ora, ricordiamo, abbiamo una serie di sensori orientabile:

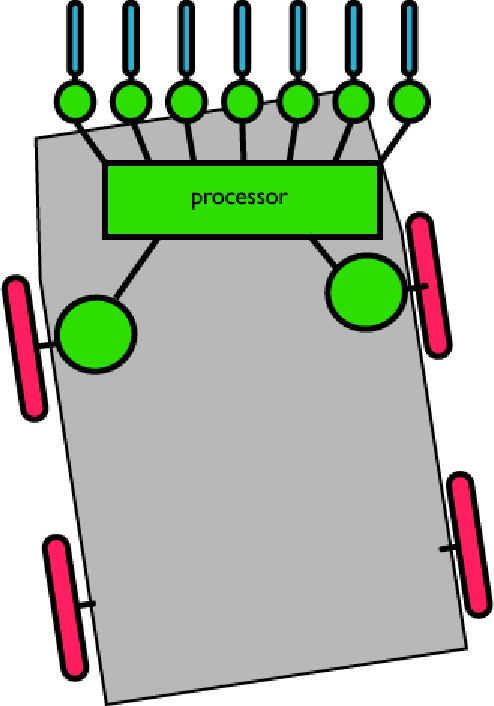
Figura 4.
Il nostro semplice carrello manterrà i suoi sensori lungo l'asse y. In questo modo è abbastanza facile calcolare l'impatto della fonte di luce sui sensori (è semplicemente la quantità di luce alla coordinata x di ogni sensore), ma questo renderà il robot un po' troppo sensibile ad ogni sorta di altri problemi. Per ora iniziamo così, e poi risolveremo la questione in seguito.

Se necessario possiamo ricaricare le matrici dei pesi salvate in precedenza:

Parametri

Stabiliremo un'arena di 20 unità di larghezza per 100 di lunghezza, una sorta di pista da bowling virtuale.

Posizioniamo manualmente la vettura e la sorgente luminosa alle due estremità del campo:

Dobbiamo anche tenere traccia dell'orientamento del robot, cioè in quale direzione puntano le ruote. Useremo la convenzione che il Nord (in alto nella corsia) è a 90° o π/2 radianti. Inoltre, avanzeremo con una velocità di 1 passo per unità di tempo e imposteremo il raggio del perno a 0.5 (quindi le ruote hanno un diametro di 1 unità):

Luce

Abbiamo bisogno di trasformare la posizione della luce in una sorta di ingresso ai sensori del robot. Dobbiamo prendere la sua posizione e trasformarla in una serie di 'luce rilevata' o 'non rilevata' per alimentare la rete. Per fare questo per questa versione dell'arena, adatteremo una distribuzione normale alla sorgente luminosa e caricheremo i sensori di conseguenza.

Allo scopo creiamo la distribuzione basata esclusivamente sulla posizione x della luce, e useremo questa come il parametro μ della distribuzione normale. Faremo inoltre diffondere la luce su un numero sufficiente di unità (ricordiamo che il 99.7% di una distribuzione normale è tra ±3σ) in modo che praticamente copra l'area dell'arena:

Ecco un grafico dell'impatto della luce su tutta la larghezza della corsia; semplicemente la funzione di distribuzione di probabilità per una distribuzione normale con i parametri specificati sopra:

Assumiamo inoltre che i sensori siano imperniati intorno al centro del robot e che siano distanti 1 unità. Quindi, in questo caso, la posizione x dei sensori sarà:

Se valutiamo la funzione di distribuzione di probabilità per la luce che abbiamo definito prima alla posizione x di ogni sensore  avremo una quantità relativa di peso su ogni sensore. Supponiamo che il sensore rilevi assenza di luce (cioè è 'off') e, come tale, ha un valore di 0.1. Aggiungeremo l'influenza della luce al valore 'off' di bias:

Questi numeri sono piccoli, ma si può vedere che sono più grandi verso destra. Ricordiamo che, quando abbiamo osservato il comportamento del nostro robot addestrato, se tutti i valori dei sensori erano 'off' (0.1) il robot si muoveva lentamente in avanti.

Gli input alla rete neurale sono tutti nell'intervallo [0, 1], ma la funzione PDF di sopra non tocca da nessuna parte questi valori. Infatti l'area sotto la distribuzione totalizza 1.0 così, per definizione, la funzione stessa dovrà rimanere al di sotto di tale valore. Per dare agli input una dinamica un po' più ampia li normalizzeremo portandoli nell'intervallo di input [[0.1, 0.9]:

Usiamo i pesi calcolati in precedenza e testiamo la rete:

Abbiamo moltiplicato il risultato per la velocità massima del robot per scalare adeguatamente i vettori di forza. Il risultato della feedForward è la velocità totale del motore sinistro e destro, rispettivamente. L'intuito ci dice che, dal momento che la luce è a destra dell'arena vogliamo che il robot sterzi a destra e, per ottenere questo risultato, la ruota sinistra dovrebbe ruotare più velocemente della destra. Infatti, l'output risultante mostra proprio questo comportamento.

La fisica reale di un robot a due ruote come il nostro è un po' più complicata di quanto non approfondiremo in questa lezione. La fisica semplificata del nostro motore assume che:

La direzione risultante θ è perpendicolare all'asse virtuale tra le due ruote.

L'asse si trasforma in funzione delle forze relative sulle due ruote in base ad una semplice soluzione triangolare.

La velocità risultante è la lunghezza media dei vettori forza delle due ruote.

In primo luogo, la parte semplice:

Quindi, la soluzione per θ. Questa soluzione è la dell'angolo formato tra l'asse e la differenza tra le due forze motrici.

Intuitivamente, questa soluzione sembra corretta. Dice al robot di ruotare in direzione negativa, cioè a destra, dove si trova la  sorgente di luce.

La nuova direzione è quella attuale più la quantità precedente:

Ora abbiamo una velocità e una direzione. Abbiamo bisogno di convertirle in coordinate rettangolari e aggiungere il risultato alla posizione attuale del carrello, e abbiamo finito (per un singolo passo).

Possiamo incapsulare la trasformazione da coordinate polari in coordinate rettangolari (ruotata per essere perpendicolare all'asse x) così:

e trasformare i risultati

Come la direzione,  la nuova posizione del robot è la vecchia posizione più questo delta:

Iteriamo!

Potremmo calcolare manualmente questi numbers ma sarebbe noioso. Possiamo invece utilizzare una Table, creando una lista di coordinate che tracciano la posizione del robot nel tempo.

Ecco le condizioni iniziali come descritto prima:

Stiamo per aggiungere altre due variabili: un semplice contatore, t, per tenere traccia del tempo, e un fattore di smorzamento . Quest'ultimo è usato per scalare i valori grezzi del motore per evitare che il carrello impazzisca e, per semplicità, è implementato come una semplice moltiplicazione, ma in realtà probabilmente dovrebbe essere parte di una media 'a finestra'. Infine tmax è utilizzato per evitare che la simulazione continui all'infinito.

Ripeteremo lo stesso processo Sow/Reap eseguito con l'accumulo di errore in teachNN. Inseriamo il tutto in un ciclo While di controllo per vedere se il tempo è trascorso o se il robot è alla stessa coordinata y della sorgente luminosa.

Al termine delle iterazioni pTable contiene un elenco di 4 valori di stato del robot per ogni passo temporale: che rappresentano il cambiamento di direzione, la direzione assoluta, il cambiamento di posizione e l'attuale posizione assoluta.

Per vedere il comportamento del cambiamento di direzione nel tempo possiamo tracciare il grafico della prima colonna in questo modo:

Quindi, per vedere la traiettoria totale del robot possiamo tracciare la colonna 4 :

Questo è un po' deludente: il robot si dirige verso la luce ma poi improvvisamente se ne allontana. Ha forse questo qualcosa a che fare con il problema dei sensori non perfettamente di fronte alla sorgente luminosa o con la direzione di marcia del veicolo?

Di nuovo!

Come si è visto, la nostra scelta della variabilità per la diffusione della sorgente luminosa ha molto a che fare con questo comportamento. Indirettamente, questo causa il problema in cui il robot non ha i sensori che puntano verso o lontano dalla sorgente luminosa.

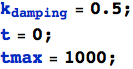
Questa volta sembra aver funzionato! Ma perché? Abbiamo armeggiato con l'ampiezza della diffusione della luce (la deviazione standard della fonte di luce).

Abbiamo a che fare con il fatto che i sensori non fanno veramente quello che vogliamo, a meno che non li ruotiamo con il carrello. Per fare questo, aggiungeremo un po' di trigonometria al modello: ciò lo complicherà un po' ma lo renderà più soddisfacente nel lungo periodo.

Da esplorare

Provare a modificare la funzione di diffusione della luce. Che effetto ha?

Riuscite a pensare a un modo per modificare il training set per rendere il robot più reattivo al nostro modello di illuminazione?

Facciamo la cosa giusta

Nel nostro precedente modello il carrello campiona la funzione di distribuzione della luce così:

Figura 5. Il nostro robot con la torretta dritta campiona la distribuzione della luce in modo non molto accettabile.

In realtà vorremmo un modello più utile che funzioni in questo modo:

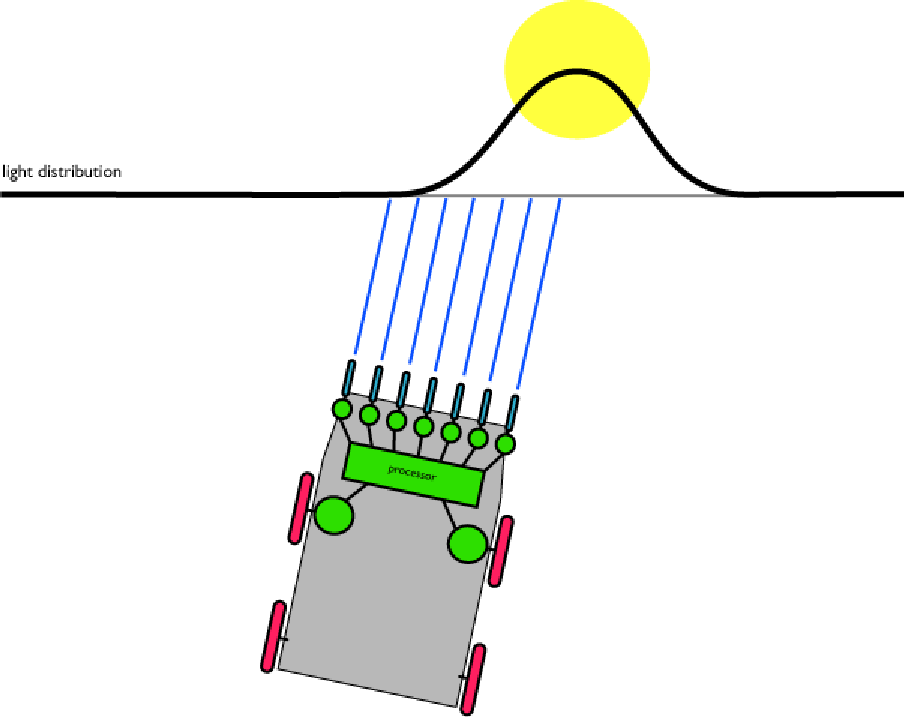
Figura 6. Il robot fotosensibile.

Questo ha molto più senso. Il robot si dirigerà verso la luce correttamente, piuttosto che comportarsi in modo strano come abbiamo visto nel modello precedente. Ciò richiede semplicemente un po' di trigonometria per ottenere le posizioni in cui le linee blu intersecano la distribuzione della luce. Dove il sensore 'guarda' dipende dall'orientamento del robot. La quantità luminosa è determinata dalla funzione di distribuzione della luce.

Applichiamo la modifica e facciamo girare il tutto.

La soluzione è implementata mediante una procedura di Mathematica:

Questa funzione ha tre argomenti: il raggio r (l'eccentricità della posizione del sensore, in pratica la distanza dal centro del robot), la direzione attuale del robot θ e la distanza dy dalla fonte di luce lungo l'asse y. Essa proietta la posizione corrente del sensore in x lungo la linea perpendicolare al carrello, verso la sorgente di luce, ed evidenzia dove colpisce l'asse x della sorgente luminosa.

Aggiunta al modello

Possiamo facilmente applicare questa modifica al nostro modello attuale sostituendo il codice che evidenzia dove siamo in x:

con qualcosa di più sensato:

Facciamo la prova.

Ecco nuovamente le nostre condizioni iniziali:

In questo caso, il robot è diretto in avanti () per cui entrambi i metodi dovrebbero fornire lo stesso risultato:

come in effetti è. Un cambiamento nella direzione:

dovrebbe causare una differenza (si noti che il robot ora punta un po' a destra):

Però! Ma quando ci si pensa un po', questo ha senso. Siamo un po' distanti ( unità in effetti) quindi l'aggiunta di 10° provoca una rotazione verso destra. Man mano che il robot si avvicina, la distanza diminuisce e l'effetto della rotazione viene attenuato.  

NB: la sottrazione di porta le coordinate del robot nello spazio giusto per la trigonometria utilizzata nella funzione project, che presuppone che tutto sia allineato lungo l'asse x, non y.

Inoltre, cerchiamo di cambiare leggermente la nostra strategia di scala. Piuttosto che lo strano parametro scale introdotto sopra, allunghiamo semplicemente la gamma dinamica di tutti i sensori per farla rientrare nell'intervallo [0.1,0.9].

Proviamolo!

Applichiamo queste modifiche e vediamo come il nostro robot si comporta ora. Avvieremo il robot con una direzione di 30° a sinistra:

Ottimo! Infatti il robot si dirige fino alla fonte di luce. Diamo un'occhiata ad alcuni dei 'delta' per vedere quello che la rete neurale diceva al robot di fare ad ogni passo.

Ecco la direzione ad ogni passo temporale:

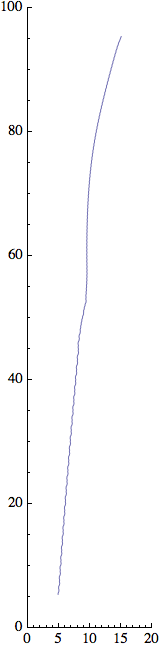
Si può vedere che ad ogni passo il robot si dirige un po' a sinistra e un po' a destra per arrivare alla luce. Attraverso gli accumuli di piccole correzioni, alla fine il robot trova la sua tana!

Queste sono le effettive direzioni prese dal robot ad ogni passo. Si noti che, all'inizio, c'è un sacco di semplice 'andirivieni'. Poi, a circa t = 150, il modello si blocca su qualcosa di più significativo e da t = 160 va liscio verso la meta:

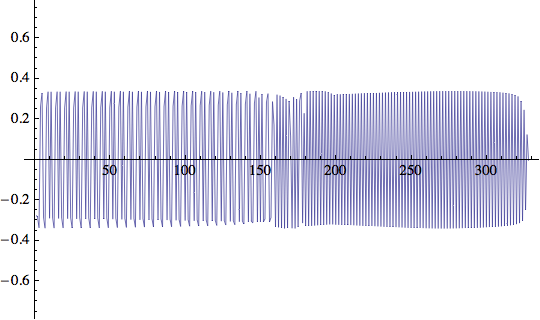
Si noti che, per tutto il tempo, il robot continua il suo andirivieni! Nel caso che la sorgente si muova (suggerimento: parte di questo comportamento è controllato da ).

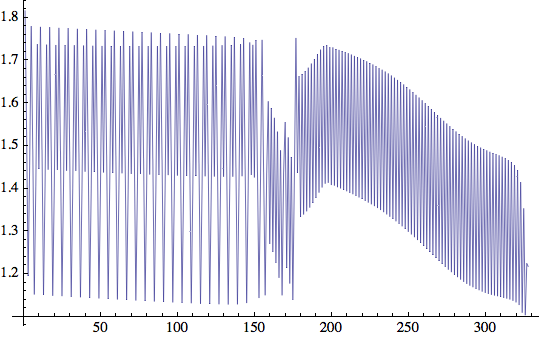
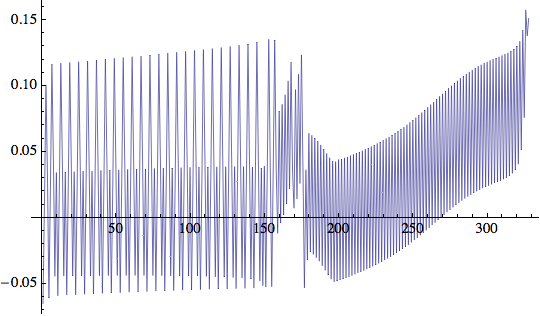
Questo comportamento è anche interessante. Ecco le correzioni alla posizione in x e y, rispettivamente:

La posizione x riflette il comportamento di scansione altalenante e la ricerca da sinistra verso destra. La posizione y indica l'esitazione iniziale e la successiva andatura 'convinta', poi l'esitazione quindi la spinta finale. Si osservi la folle corsa in avanti negli ultimi passi!

Da esplorare

Manipolare il fattore di smorzamento. Questo ha un forte effetto sui modelli di comportamento di cui sopra. Perché?

Aggiungere rumore alle varie parti del sistema. Ai sensori (letture e posizione), la sorgente luminosa (lettura e posizione), i controller del motore.

Aggiungere un'altra sorgente luminosa.

Insegnare al robot ad evitare fonti di luce, aggiungere diverse sorgenti luminose.

Muovere le luci

Il robot converge abbastanza bene su un bersaglio fermo. Può tenere traccia di un bersaglio mobile con precisione? Facciamo la prova con l'aggiunta di qualche moto browniano alla posizione della luce! Sarà il robot ancora in grado di trovarla?

Vedo una piccola luce…

La stessa inizializzazione.

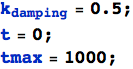
Aggiungiamo un fattore di jitter (movimento irregolare):

quindi, durante ciascuna iterazione, muoveremo di una quantità casuale, cioè

Tutto il resto è immutato.

Si noti che abbiamo aggiunto alla lista di output in posizione 5. Ecco un grafico del movimento della luce:

Ed ecco il movimento del robot. Sembra che si comporti molto bene:

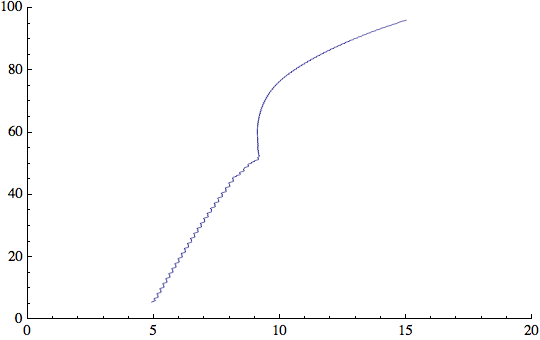
In effetti, guardando l'ultima iterazione, gli ultimi due valori in pTable (la posizione del robot e della luce) sono molto vicini.

Più disturbo

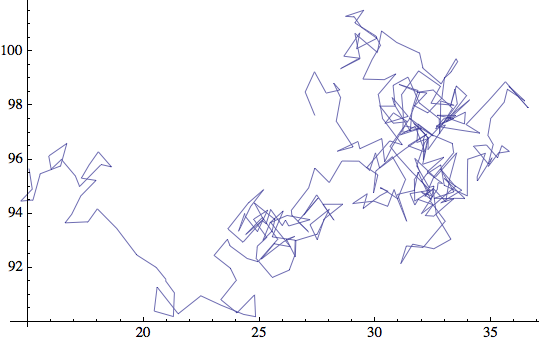
Aggiungiamo più jitter, 10 volte tanto:

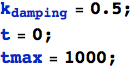
Bel lavoro.

Andiamo oltre?

OK, un altro ordine di grandezza:

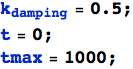
Incredibile! La sorgente di luce ha vagato qui e là ma è ancora stata rintracciata. Questi robot sono robusti!

Da esplorare

Fin dove possiamo spingerci?

Come influenza lo smorzamento questo modello? Tracciare i vari θ per verificarlo.

Battaglia di robot!

Immaginiamo il seguente scenario: due robot, ognuno con una luce sulla parte superiore, ciascuno che cerca l'altro! Saranno in grado i nostri robot ciascuno di trovare l'altro?

Dobbiamo fare alcune piccole modifiche. In primo luogo, elimineremo la variabile della sorgente luminosa dal momento che entrambi i robot sono sorgenti luminose. Creeremo una lista di posizioni e orientamenti:

Per ora lasceremo il resto inalterato.

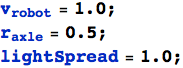
Si potrebbe eventualmente spostare lo smorzamento nello stato di ogni robot, ma non per ora...

Per raggiungere il nostro obiettivo ripeteremo due volte in ogni passo il processo 'individua-calcola-rispondi'; una volta con il primo robot come  cacciatore e il secondo robot come obiettivo (luce), poi nuovamente a ruoli invertiti. Per il primo tentativo:

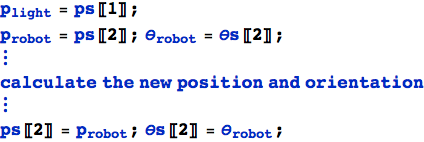
Non dimentichiamo di salvare la posizione e l'orientamento nei robot. Poi, per la seconda iterazione scambiamo i ruoli:

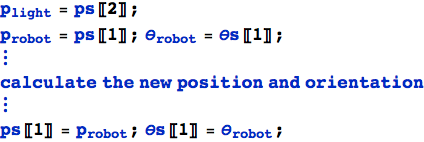
Ci sbarazzeremo del controllo della distanza y in quanto ora vi sono più robot posizioni luminose. Ci limiteremo ad eseguire per tmax iterazioni.

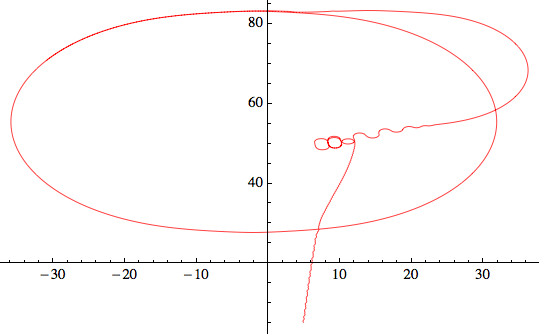
Tracciamo la traiettoria del primo robot (si noti che pTable è stata semplificata per questo esperimento; contiene solo le posizioni dei robot).

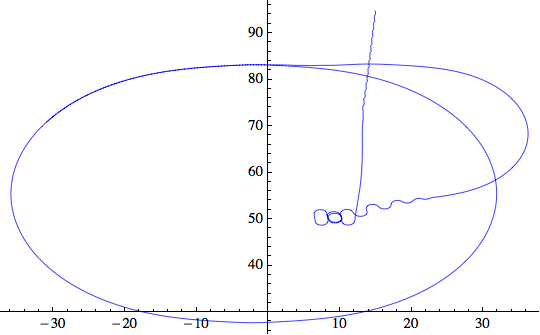
Molto interessante: entrambi partono verso l'altro e quindi iniziano una sorta di danza di avvicinamento. Come è probabile, stiamo osservando un comportamento complesso di un sistema molto semplice. Un buon punto da discutere.

Dove sono i robot dopo le 1000 iterazioni?

Sono molto molto vicini l'uno all'altro. Si potrebbe eseguire la simulazione per un tempo più breve per vedere il comportamento più da vicino. Un'altra opzione è quella di tracciare una animazione del processo. Il codice qui sotto traccia i primi 500 passi del movimento dei robot. Un robot è rosso, l'altro blu. Ciascuno lascia un 'coda' di 30 unità (la variabile win controlla questo aspetto) e ogni fotogramma rappresenta 10 unità di tempo (la variabile lag controlla questa situazione). Se si ha molta pazienza è possibile rimpicciolire lag e impostare le iterazioni a 1000 invece che 500.

Per visualizzare l'animazione, basta cliccare sul triangolo nero della finestra di animazione:

L'animazione mostra che i robot vanno l'uno dritto verso l'altro, quindi iniziano a girare l'uno intorno all'altro in quella che sembra davvero essere una danza!

Da esplorare

Aggiungere rumore ai sensori ed al sistema: questo cambia il comportamento, in particolare della danza finale?

Si può provare a modularizzare il codice per gestire più robot, sorgenti luminose statiche, etc.

Provare a far muovere i robot attraverso un labirinto. È possibile applicare qualche semplice rilevamento di collisione (che era l'obiettivo originario dell'arena, avere confini elastici attorno ad essa per mantenere il robot in campo) e vedere se il robot può imparare un labirinto. Ancora meglio, si può far evolvere il robot addestrandolo sul riconoscimento di alcuni pattern alcuni come abbiamo già fatto (un gradiente di luce semplice), provarlo e utilizzare i risultati per dare alla rete ulteriore addestramento!

Utilità generali

Disattivo i warning

Imposto la directory corrente

Created with Wolfram Mathematica 7.0