Università di Foggia

Dipartimento di Scienze Biomediche

Prof. Crescenzio Gallo

c.gallo@unifg.it

Reti neurali artificiali con Mathematica

Apprendimento e adattamento dei pesi

Lezione 4

Introduzione

Nelle lezioni precedenti abbiamo discusso le interazioni di pesi e ingressi sugli output risultanti del neurone artificiale e abbiamo modificato manualmente i pesi e le soglie per ottenere il risultato che volevamo. I neuroni artificiali che abbiamo discusso in precedenza [1,2,3] hanno parametri regolabili (i pesi di ingresso, α) che abbiano calcolato manualmente. Possiamo automatizzare questo processo in qualche modo?

Come 'apprendono' e si adattano i neuroni del nostro cervello?

Hebb

Nel 1949 Hebb fece la seguente osservazione sui neuroni biologici:

Quando l'assone di una cellula A è abbastanza vicino da eccitare una cellula B e ripetutamente o persistentemente partecipa alla sua attivazione, si verifica un qualche processo di crescita o cambiamento metabolico in una o entrambe le cellule tale che l'efficienza di A, quale una delle cellule che attivano B, viene accresciuta. [4]

Tale osservazione può essere graficamente dimostrata nel modo seguente:

Figura 1. Due neuroni, A e B. Assumiamo che anche altri neuroni convergano su B.

Abbiamo qui due neuroni A e B. In realtà vi sarebbero diversi altri neuroni in ingresso a B (e ad A). Visualizziamo qui una sinapsi eccitatoria, ma in teoria sanche una sinapsi inibitoria funziona allo stesso modo.

Figura 2. Assumiamo che A (insieme ad altri neuroni) attivi B.

L'idea qui è che A, insieme ad altri neuroni, attivi B. Ma ogni volta che A si attiva, anche B si attiva.

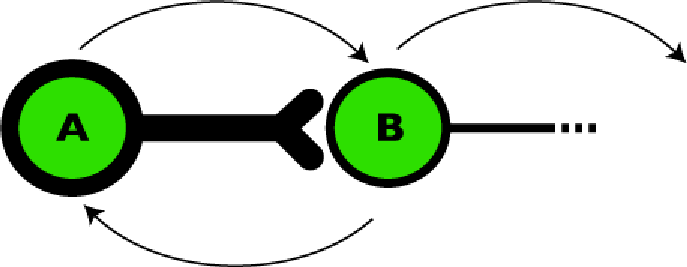
Figura 3. Assumiamo che l'attivazione di A e B si verifichi congiuntamente, cioè che ogni volta che A si attiva B fa altrettanto.

Inizialmente B può richiedere un input significativo da A per attivarsi. Ma appena si ripetono le attivazioni contemporanee...

Figura 4. Le attivazioni di A e B si rafforzano reciprocamente.

...le attivazioni ri rafforzano reciprocamente.

Figura 5. Come risultato, A richiede meno ‘sforzo’ per attivare B (insieme agli altri neuroni).

Conseguentemente, la sinapsi tra A e B richiederà meno 'lavoro' per provocare l'attivazione di B.

Questa è una bella notizia per i nostri neuroni biologici. Infatti, a pensarci bene, è una sorta di comportamentismo; più specificamente, una specie di apprendimento rinforzato. Quando A e B si accoppiano si forma un'associazione.

Apprendimento artificiale di Hebb

Possiamo tradurre la precedente descrizione biologica nel nostro mondo artificiale? L'idea generale è la seguente:

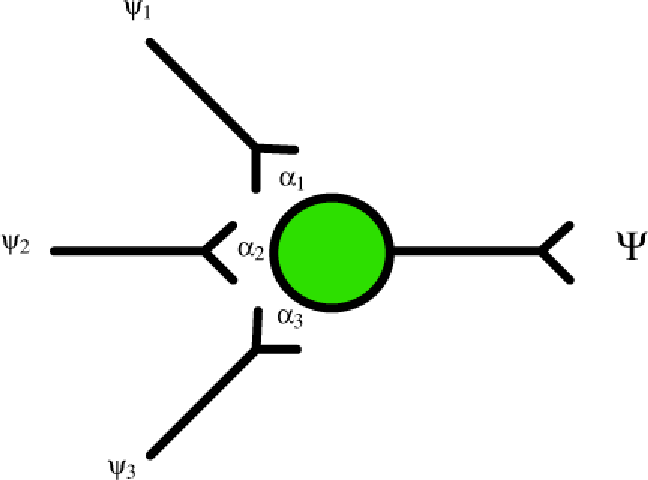
Figura 6. Un neurone simulato con input ψ, pesi α e output Ψ.

Immaginiamo che il nostro neurone artificiale con il vettore di input ψ sia l'output di altri neuroni collegati. Supponiamo che i pesi α rappresentino l'efficienza della sinapsi. Più efficiente è la sinapsi (cioè maggiore è ) più probabilmente un ingresso positivo farà sì che il neurone si attivi. Si noti che questo può funzionare come un meccanismo sia eccitatorio che inibitorio. Valori negativi inibiscono l'attivazione finale, ipotizzando un ingresso positivo.

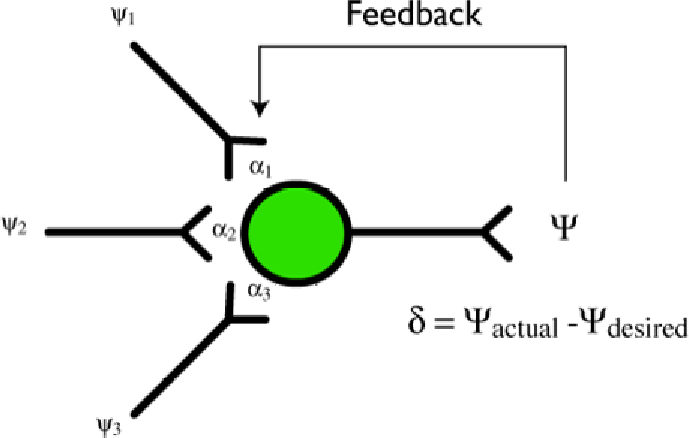
Figura 7. Dopo l'attivazione del neurone, possiamo esaminare l'output Ψ ottenuto e confrontarlo con quello desiderato. La differenza δ può essere usata per meglio assicurarsi che l'output Ψ sia più vicino al valore desiderato.

Utilizzando un meccanismo noto in genere come feedback possiamo adattare il nostro vettore dei pesi. L'idea di base del meccanismo è quello di calcolare la differenza tra ciò che è stato ottenuto ed il valore  desiderato, δ nella figura sopra, e usare questo valore per regolare α per riprodurre meglio il valore desiderato.

Figura 8. Immaginiamo uno scenario nel quale l'input coincide frequentemente con l'attivazione del neurone.

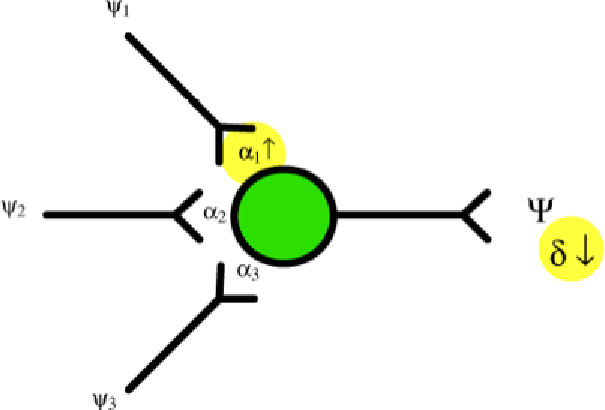
Figura 9. Attribuendo ad un peso maggiore si riduce l'errore δ tra l'output teorico e quello ottenuto.

Se vediamo un modello di comportamento come quello mostrato sopra, possiamo adattare i pesi per minimizzare l'errore δ. Ad esempio, se il neurone si attiva con l'input possiamo dare a questo input un peso maggiore per facilitare il processo. Ed è proprio quello che faremo.

Trovare una soluzione

È interessante notare che le cellule artificiali e i processi che abbiamo utilizzato fino a questo punto sono lineari. Il prodotto scalare comporta la moltiplicazione e addizione, l'essenza dell'algebra lineare. Una caratteristica molto piacevole dei sistemi lineari è che è abbastanza semplice trovare soluzioni ai problemi lineari direttamente quando l'informazione è sufficiente.

Esaminiamo una semplice situazione nella quale abbiamo un set di input dati e vorremmo che il neurone artificiale produca un particolare output. Possiamo fare questo in una sorta di approccio a forza bruta con un po' di manipolazione algebrica.

Prendiamo un arbitrario vettore di input ψ ed un valore di output desiderato Ψ:

Ora creiamo una lista casuale di n-1 pesi ed aggiungiamo alla fine un peso ‘sconosciuto’ ζ:

Il loro prodotto scalare è

Risolviamo facendo uso della funzione Solve[]:

In tal modo abbiamo determinato il peso mancante. Solve[] restituisce una lista di regole di sostituzione per l'equazione fornita. Il comando /. applica regole ad un'espressione, sostituendo la parte a destra della freccia → nell'espressione di sinstra:  

Ora possiamo controllare il nostro lavoro, facendo il prodotto scalare del vettore di input e dei pesi:

o, alternativamente:

Ok. Abbiamo addestrato la nostra rete per produrre un semplice output dato un particolare input. Ma abbiamo bisogno di qualcosa di più flessibile. Vorremmo un sistema con più controllo sugli input e gli output.

Ad esempio, per i nostri problemi AND, OR e XOR abbiamo avuto bisogno di specificare i risultati di 4 differenti set di 2 input ed i relativi 4 output desiderati. Di seguito vedremo un tipo più generalizzato di apprendimento.

Errore

Prima di esaminare il caso multidimensionale esaminiamo l'idea di errore nelle nostre previsioni. In generale possiamo pensare all'errore come la differenza tra la previsione del nostro modello e il valore desiderato. Per esempio, nel modello lineare

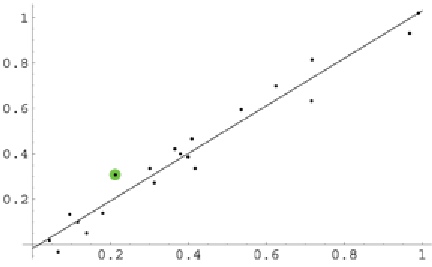
Figura 10. Il modello lineare y=1.05x-0.02

il valore evidenziato per x=0.21 è ben al di sopra della retta; infatti, l'errore è

così nel nostro caso

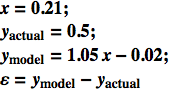
possiamo dire che il modello sottostima il risultato reale di circa 0.3.

Si può vedere che l'errore in questo caso è negativo. Notiamo che ci sono più coppie (x, y) nell'esempio precedente. Ogni x ha la propria y e il modello predice una y anch'esso. Se dovessimo sommare tutti gli errori nel grafico ci sarebbero molti punti sopra (errori negativi) e molti sotto (errori positivi). Sommandoli tutti tenderebbero a 0. In realtà, siamo interessati alla grandezza dell'errore. Potremmo sommare il valore assoluto di tutti gli errori ma faremo invece la cosa statisticamente corretta calcolando i quadrati degli errori: in pratica, l'errore quadratico medio (MSE, Mean Square Error) o varianza.

Quindi, ciò a cui siamo interessati è:

per tutte le coppie (x,y). Questo ci fornisce la grandezza media assoluta dell'errore quadratico.

Neuroni artificiali

Cosa dire sulla situazione del neurone simulato?

Immaginiamo un neurone con due input il quale, ogni volta che il vettore di input vale ψ={10,3} produce l'output desiderato Ψ=42. (NB: per ora stiamo semplicemente parlando di un generico neurone artificiale senza soglia, uno che produce giusto la sommatoria degli input pesati). Per questa simulazione occupiamoci di questo unico input, tralasciandone per ora eventuali altri. Quale sarà l'errore man mano che i pesi variano? Possiamo vederlo facilmente con un grafico. La formula cui siamo qui interessati è l'errore visto prima; sviluppandolo abbiamo:

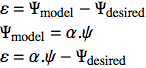
Abbiamo bisogno di calcolarlo per ciascuna coppia di input/output, farne il quadrato e sommarlo secondo l'equazione 2.

Diamo un'occhiata ad un grafico dell'errore in presenza di una singola coppia di input/output. Dato che c'è un solo elemento, possiamo semplicemente fare il quadrato dell'errore calcolato secondo l'equazione 3 precedente senza fare la somma. Esamineremo una situazione nella quale il nostro input è ψ={10,3} e l'output desiderato è Ψ=42. Faremo il grafico dell'errore ε in funzione di tutti i possibili vettori dei pesi α i cui elementi appartengono all'intervallo (-10,10):

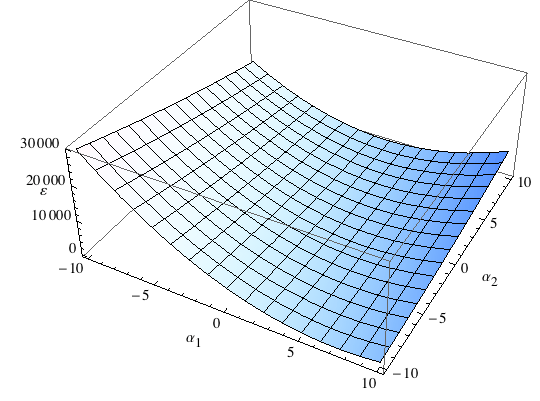
Il grafico risultante è la cosiddetta superficie di errore — la sua altezza sullo zero rappresenta l'errore totale ε per un dato α. Se si osserva attentamente si vede che vi sono 'alcune' posizioni (in realtà infinite) dove l'errore è 0. Queste sono le soluzioni per i pesi α che ci forniranno il risultato desiderato (cioè per le quali l'output della rete coincide con quello atteso).

Esempio

Troviamo la soluzione al nostro problema dei pesi mediante la funzione Mathematica Solve[].

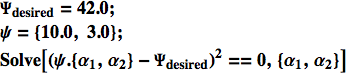
Osserviamo che, essendovi due gradi di libertà ed una sola equazione, abbiamo le soluzioni per in termini di : la solzione è cioè inderdeterminata.

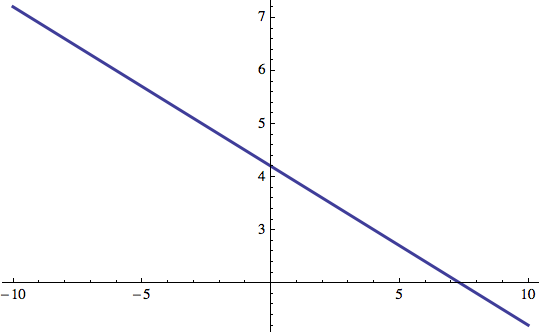
Output multipli

Il nostro problema diventa un po' più complicato se vogliamo mappare un insieme di input potenziali verso un insieme di output correlati. I problemi AND OR e XOR discussi in precedenza sono buoni esempi di questa situazione.
Vogliamo quindi qualcosa che possa rispondere a due differenti set di input in due differenti modi. Torneremo alla precedente coppia di input/output e ne aggiungeremo un'altra che risponde con 18.5 quando gli input sono {3,6}:

Lo chiamiamo training set, in cui ciascuna riga consiste di un input e del relativo output desiderato.

Per mezzo della funzione Map[] possiamo calcolare l'errore per un dato vettore α:

Qui ciascuna riga del training set viene data in ingresso alla funzione pura nel primo argomento del comando Map[]. Il primo elemento di ciascuna riga del training set è l'input, e viene 'recuperato' con il suffisso [[1]]; il secondo è il risultato atteso, estratto mediante [[2]].

Ora che abbiamo i singoli termini dell'errore possiamo addizionarli per mezzo di Apply[] e Plus[] e quindi dividere il risultato per il numero di elementi per ottenere l'errore finale:

Visualizziamo il grafico della superficie di errore:

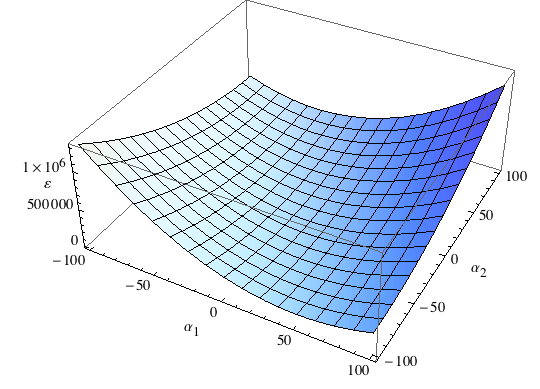
In questo caso si vede che c'è una sola posizione sulla superficie di errore con ε=0. Cerchiamo un metodo generale per trovare tale soluzione.

Esempio

Possiamo trovare i pesi corrispondenti all'errore minimo applicando le nozioni dell'algebra lineare. In sostanza, per risolvere l'equazione ψ.α = Ψ facciamo uso della matrice inversa nel seguente modo: ψ.α = Ψ da cui α = Ψ.

   Mediante la funzione MapThread[] possiamo quindi trovare la lista degli errori:

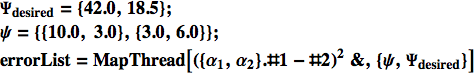
Il comando MapThread[] ha come primo argomento una funzione e la applica a ciascun elemento della lista fornita come secondo argomento.
Una volta ottenuta la lista degli errori quadratici, ne facciamo la media ottenendo il Mean Squared Error:

Visualizziamo la superficie dell'errore:

   Possiamo ottenere lo stesso risultato facendo uso della funzione FindMinimum[] di Mathematica:

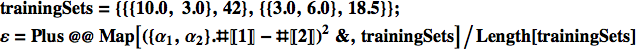
La regola Delta

Abbiamo appena visto quello che potremmo fare se avessimo un'idea fissa sugli ingressi e le uscite che vogliamo associare. Supponiamo per un momento che ci piacerebbe una soluzione ancor più generale al problema di cui sopra. Una soluzione in cui ψ e Ψ possano variare nel tempo, ad esempio. Abbiamo bisogno di progettare un sistema che, in un certo senso, impari dagli esempi presentati. Questo tipo di addestramento si chiama apprendimento supervisionato, un tipo di apprendimento dove vengono presentati esempi di ciò che si inserisce nella rete e del risultato desiderato, regolando di conseguenza i pesi.

Avrete notato che abbiamo appena aggiunto una variabile interessante, il tempo. Stiamo per cambiare lo stato del nostro sistema (cioè i valori dei pesi) nel corso del tempo, e in funzione dell'errore. Algoritmicamente, stiamo per fare quanto segue:

Al tempo (iniziale) assegniamo un set arbitrario di pesi ad α

Mediante il valore corrente di α, calcoliamo ε

Adattiamo α per ridurre ε

Incrementiamo il tempo e ripetiamo dal passo (2)

Questo può essere rappresentato mediante la seguente relazione ricorsiva:

In parole povere, il vettore dei pesi al tempo t+1 è uguale al vettore dei pesi corrente più una frazione dell'errore. Questa frazione, η, è chiamata tasso di apprendimento (learning rate).

Se ripetiamo sufficientemente questo processo, cioè se addestriamo la nostra rete con un numero sufficiente di esempi, possiamo presentare un nuovo input al sistema e misurare il relativo output. Come abbiamo fatto per la regressione lineare, abbiamo creato un modello che può essere utilizzato per predire e testare.

Un semplice esempio

Consultare il testo di Freeman [5] per una panoramica più completa.

Ecco un esempio molto semplice di apprendimento con la regola delta.

Esaminiamo una particolare situazione di input, utiizzando la funzione OR discussa in precedenza. Per l'input:

(1)

vorremo avere l'output:

(2)

Possiamo impostare il sistema con:

Ora abbiamo bisogno di un set di pesi per il nostro vettore di input. Creiamo due valori a caso:

Vediamo che output otteniamo:

Il nostro errore sarà:

Non proprio accettabile...

Calcoliamo il δ (in sostanzaa un ‘fattore di correzione’) con l'equazione:

Stiamo in pratica scalando l'errore per mezzo del fattore (output(1-output)). Questo termine possiede un interessante comportamento parabolico:

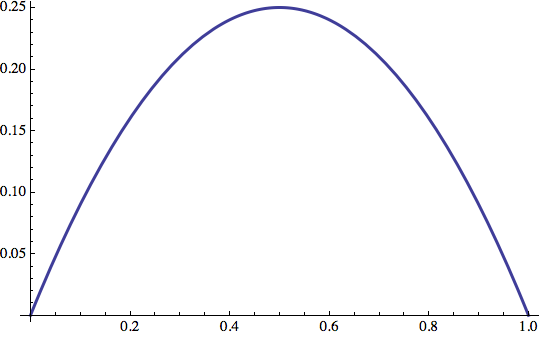
in modo che i valori verso il centro dell'intervallo vengono amplificati mentre quelli verso i bordi sono diminuiti. Il nostro delta sarà quindi:

Infine, scaliamo il vettore dei pesi α di una frazione di δ. Tale frazione, η, è il tasso di apprendimento già visto prima. Impostiamo η ad un valore piccolo:

in modo che il fattore finale di scala sia:

Per incrementare α scriveremo:

Con questo nuovo vettore dei pesi quale sarà il nuovo output e, soprattutto, l'errore sarà diminuito?

L'output precedente 0.335104 era leggermente inferiore: ci stiamo pian piano avvicinando all'output desiderato Ψ = 1.

Ripetiamo il processo tenendo traccia dell'errore. Possiamo iterare facilmente per mezzo della funzione Table[]:

Ciascun comando separato da un ‘;’ è un calcolo utilizzato successivamente. La variabile ε alla fine viene quindi aggiunta, ad ognuna delle 500 iterazioni, alla fine della lista εList.
Ecco un grafico dell'errore in funzione del tempo:

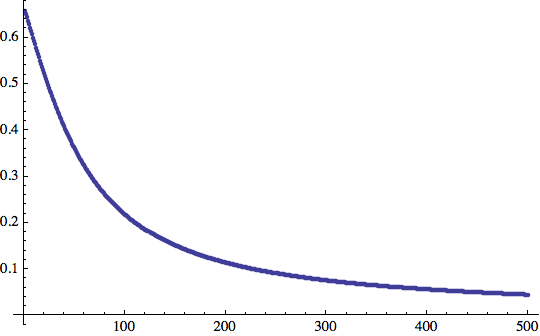
Qual è ora il valore del vettore dei pesi?

E l'output?

Abbastanza vicino a 1.

È istruttivo osservare la cosiddetta traiettoria del vettore alfa nel tempo. Ecco un esempio. Invece dell'errore ε ad ogni iterazione, esamineremo il vettore α (iniziamo con un nuovo vettore dei pesi):

Ecco le prime 30 coppie di α:

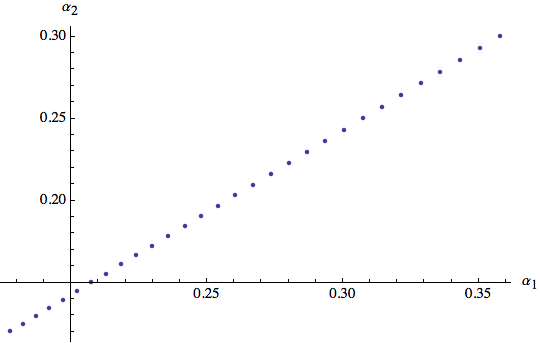
il vettore α finale e l'output:

Si vede come α tenda al suo obiettivo finale.

Apprendere in presenza di rumore

Proseguiamo il nostro esempio precedente con una variazione interessante — cosa succede quando si introduce rumore in varie parti del sistema? Per esempio, immaginate un collegamento difettoso tra gli ingressi e i pesi associati. Durante ogni iterazione, l'ingresso {0,1} varia un po'. Il sistema può ancora imparare e regolare il vettore α?

Possiamo simularlo semplicemente aggiungendo un disturbo al vettore di input ad ogni iterazione per mezzo della funzione Random[]:

Immaginate una connessione 'difettosa', dove vengono aggiunti un po' di bit di rumore durante ogni passo.

Ecco il vettore random dei pesi

ed il nuovo codice di iterazione. Questa volta prenderemo due piccioni con una fava, e costruiremo una tabella con sia il vettore dei pesi che l'errore per ogni passo:

Ecco il vettore dei pesi:

e l'output risultante:

Questo è il grafico dell'errore:

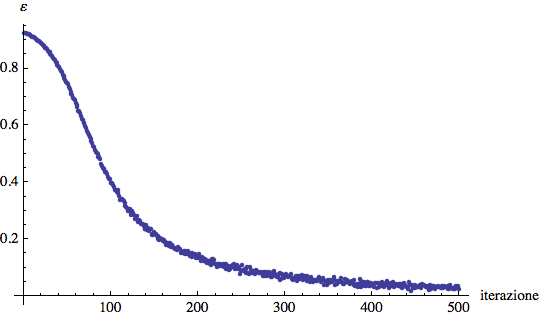
e dei pesi per le ultime 50 iterazioni:

Quindi, in sostanza, anche in presenza di rumore, il sistema sembra fare un buon lavoro.

Bibliografia

   [1]   McCulloch, WS, Pitts, W. 1943, 'A logical calculus of the ideas immanent in nervous activity', Bulletin of Mathematical Biophysics, vol. 5, pp 115–133.

   [2]   Rosenblatt, F. 1959, ‘Two theorems of statistical separability in the perceptrton’, Proceedings of a Symposium on the Mechanization of Thought Processes, Her Majesty's Stationary Office, London, pp. 421–456.

   [3]   Rosenblatt, F. 1962, Principles of Neurodynamics, Spartan Books, New York.

   [4]   Hebb, DO. 1949, The Organization of Behaviour, Wiley, New York.

   [5]   Freeman, JA. 1994, Simulating Neural Networks with Mathematica, Addison-Wesley, Reading MA.

Appendice

Utilità generali

Disattivo i warning

Created with Wolfram Mathematica 7.0