Università di Foggia
Dipartimento di Scienze Biomediche
Prof. Crescenzio Gallo

c.gallo@unifg.it
Reti neurali artificiali con Mathematica
Usiamo i neuroni
Lezione 3
Introduzione
Ora che abbiamo visto come fare i calcoli di base per un percettrone, proviamo a costruirne uno che faccia qualcosa di utile.
Teorie razionali della mente recitano che gran parte del pensiero è riducibile ad una serie di predicati a cui può essere applicata l’analisi logica formale. Mettete abbastanza di questi operatori logici insieme e otterrete un sistema in grado di prendere decisioni (o un computer). Esploreremo alcune funzioni logiche tradizionali e vedremo come progettare un set di pesi in ingresso per fare comportare il nostro neurone artificiale come le funzioni logiche.
L’AND logico
La funzione logica AND confronta i suoi due (predicati di) input: se sono entrambi veri (‘1’) la funzione restituisce vero (‘1’), altrimenti falso (‘0’). La tavola di verità della funzione AND è la seguente:
| out | ||
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Tabella 1. Tavola di verità della funzione AND.
L’AND ha un’uscita (Ψ) che vale 1 se, e solo se, tutte le componenti del vettore di input (ψ) valgono anch’esse 1. Altrimenti l’output è 0.
Nella notazione della logica matematica, l’AND viene tipicamente scritto
|
| (1) |
Possiamo immaginarla come un neurone con due input:
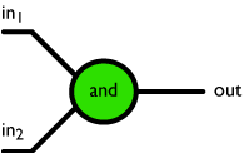
Figura 1. Il neurone artificiale AND.
Osserviamo che in=ψ e out=Ψ.
Basandoci su quanto fatto in precedenza, possiamo trovare un set di pesi per gli input che ricreino il comportamento la funzione AND?
Realizzare l’AND
Questi sono i possibili stati di input:
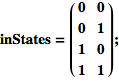
Possiamo descrivere i quattro stati di input graficamente nel seguente modo:
![]()
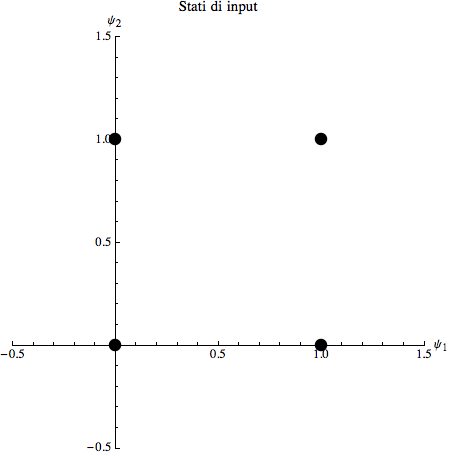
Per ottenere un neurone che si comporti come una funzione AND abbiamo bisogno di partizionare lo spazio degli input in due insiemi: una serie di ingressi che dovrebbe restituire ‘0’ e un altro set che dovrebbe restituire ‘1’.
La funzione StatePlot[], definita di seguito, ci permette di tracciare gli stati d’ingresso con le loro uscite (desiderate). La funzione accetta due parametri, un elenco degli stati di ingresso e un elenco dei corrispondenti stati di uscita desiderati. Le uscite (Ψ) con valore ‘1’ sono rappresentate come punti solidi, le uscite ‘0’ da cerchi vuoti.
Per la funzione AND, secondo la tabella di verità di cui sopra, tutte le uscite sono ‘0’ a meno che entrambi gli ingressi siano ‘1’:
![]()
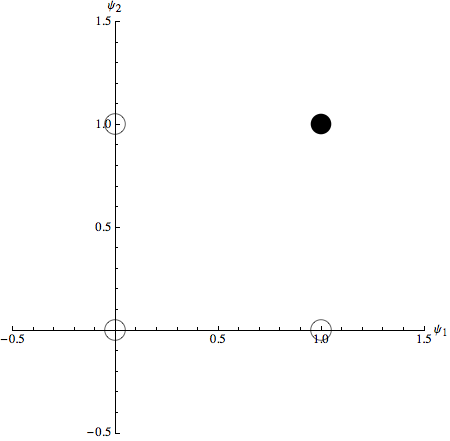
Una possibile retta (definita tramite due suoi punti) che partiziona gli stati di input nei due possibili valori ‘0’ e ‘1’ è la seguente:
![]()
ed ecco la rappresentazione visiva della separazione degli stati di input:
![]()
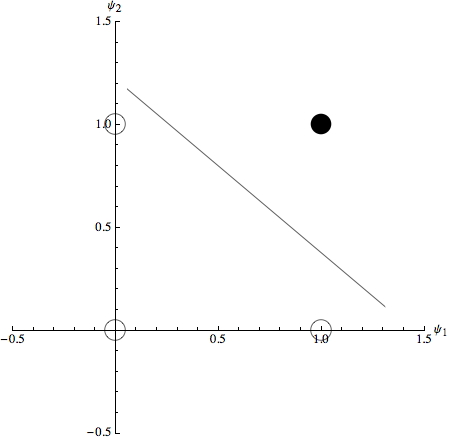
Gli stati sopra la retta di separazione corrispondono a quelli che attivano il neurone, cioè ψ={1,1} con Ψ=1, mentre quelli al di sotto restituiscono un’uscita zero (Ψ=0).
Se abbiamo l’equazione della retta possiamo scrivere una sorta di funzione criterio per decidere se un input è al di sopra o al di sotto. Per fare questo possiamo utilizzare la forma esplicita dell’equazione della retta:
|
| (2) |
Ecco come trovare l’equazione dai dati a disposizione.
1. Calcoliamo dx e dy:
![]()
![]()
2. Calcoliamo il coefficiente angolare a:
![]()
![]()
3. Determiniamo l’ordinata all’origine b utilizzando uno dei due punti:
![]()
![]()
L’equazione della nostra retta di separazione sarà quindi:
|
| (3) |
Fatto questo, ora ci occuperemo dei pesi per gli input.
Aggiunta di una soglia
Apportiamo una piccola modifica alla nostra funzione:
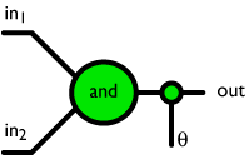
Figura 2. Il neurone AND con una funzione soglia.
Abbiamo aggiunto un parametro θ all’output, la soglia, simile alla funzione a gradino (‘step function’) vista in precedenza. Qui in valore di soglia è parametrizzato, a differenza della semplice funzione a gradino:
![]()
In Mathematica, questa funzione può essere rappresentata da:
![]()
Ecco un esempio di ![]() [] con θ = 0.5:
[] con θ = 0.5:
![]()
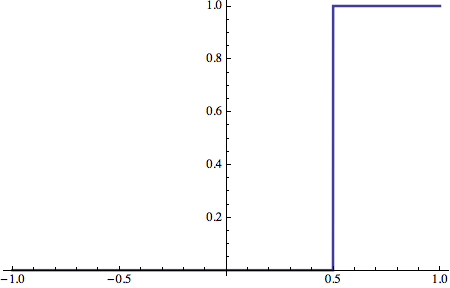
Mediante il parametro θ possiamo ora procedere a costruire un insieme di pesi tali che, applicando {1,1} agli input otterremo un output ‘1’, e ‘0’ in tutti gli altri casi.
Ricordiamo l’equazione della retta di separazione y=ax+b=-0.844x+1.221.
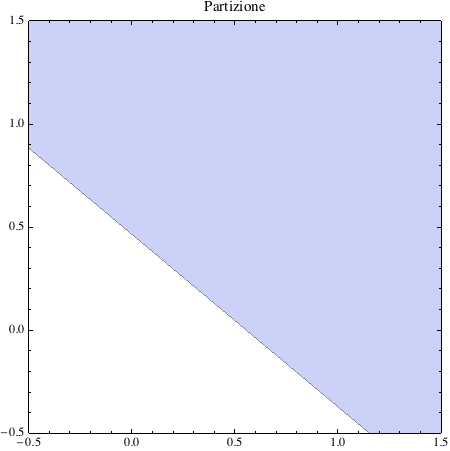
Evidenziamo la parzitione dello spazio degli input:
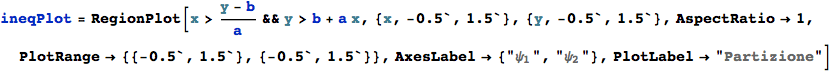
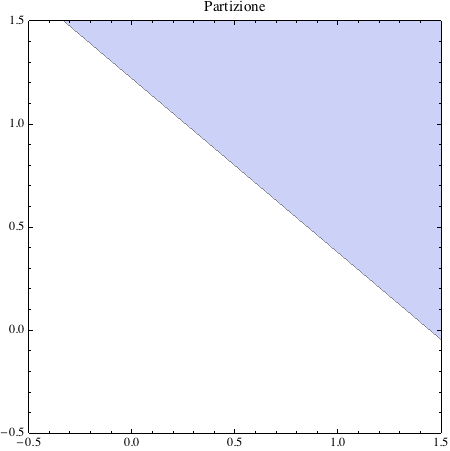
e verifichiamo che i punti dello spazio di input vi siano contenuti:
![]()
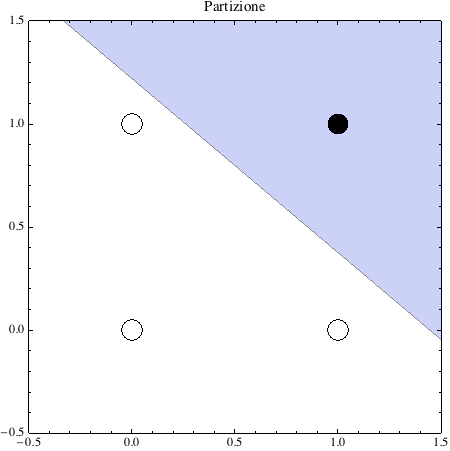
Assegniamo i pesi (il vettore α) agli input associando il (valore assoluto del) coefficiente angolare ad un input, e 1 all’altro:
![]()
![]()
La soglia sarà l’ordinata all’origine:
![]()
![]()
Fondamentalmente, l’idea è questa: quando entrambi gli input sono ‘1’ la somma degli input pesati sarà più grande del valore dell’ordinata all’origine, la soglia θ.
Utilizzando la funzione ![]() possiamo decidere se il valore supera o meno θ ed agire di conseguenza.
possiamo decidere se il valore supera o meno θ ed agire di conseguenza.
Ricordiamo che la variabile inStates contiene l’insieme dei possibili vettori di input. Vogliamo testare ciascuno singolarmente.
In Mathematica, gli elementi di una lista (vettore) possono essere estratti mediante l’operatore [[]]. Quindi, per testare il primo input:
![]()
![]()
ne facciamo il prodotto scalare con il vettore α dei pesi:
![]()
![]()
Sembra che funzioni. Infatti, 0×0.844 + 0×1.0 = 0. Ora possiamo applicare la funzione di attivazione a soglia per verificare l’output:
![]()
![]()
Quindi, per il vettore di input ψ={0,0} l’output è Ψ=0 (che corrisponde al valore desiderato come si può verificare in Tabella 1). Controlliamo gli altri input:
![]()
![]()
![]()
![]()
Gli input {0,1} e {1,0} entrambi forniscono 0, come da Tabella 1. L’ultimo input, {1,1}:
![]()
![]()
dà 1, proprio come ci aspettavamo.
Testing automatico
Possiamo automatizzare il procedimento manuale precedente.
La funzione Map[] (anche indicata con '/@') consente di applicare una funzione a diversi input.
Nel seguente esempio, vengono presi gli elementi di inStates nell’ordine (# indica il singolo elemento mentre & denota una funzione pura, che non necessita di essere definita a parte):
![]()
![]()
Esaminando gli output insieme ai vari input, verifichiamo di aver utilizzato i pesi giusti:
![]()
| in1 | in2 | out |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Perfetto! Abbiamo ora un insieme di pesi ed un valore di soglia funzionanti.
Altre funzioni booleane
Oltre all’operatore logico AND, vi sono molte altre funzioni della form x ◦ y = z con x,y,z∈{0,1}. Infatti, vi sono ![]() tali possibili funzioni (il numero totale di modi di disporre i 4 output binari). Esaminiamone una in particolare: la funzione logica (operatore) OR.
tali possibili funzioni (il numero totale di modi di disporre i 4 output binari). Esaminiamone una in particolare: la funzione logica (operatore) OR.
L’operatore OR restituisce ‘1’ se almeno uno dei due input è ‘1’, ‘0’ altrimenti.
la tavola di verità è la seguente:
| out | ||
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Tabella 2. Tavola di verità dell’OR.
In notazione matematica l’OR si scrive:
|
| (4) |
Esercizio.
Possiamo utilizzare la stessa tecnica vista prima per costruire un neurone che restituisca l’appropriato valore in corrispondenza dell’input.
Soluzione
![]()
![]()
![]()
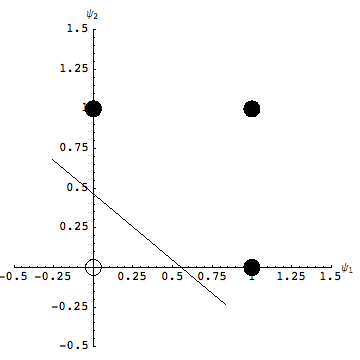
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
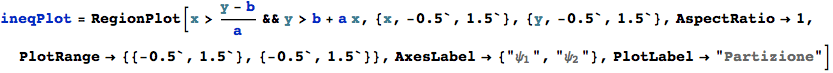
![]()
![]()
| in1 | in2 | out |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
XOR
Le funzioni logiche come queste sono le basi matematiche del moderno calcolo digitale. Combinazioni di AND, OR, e simili sono assemblate per svolgere le funzioni di base di quasi tutti i dispositivi informatici moderni.
Cosa succede se modifichiamo la funzione OR per restituire ‘1’ solo se uno dei due ingressi vale ‘1’, ma non entrambi?
La nostra nuova tabella di verità è la seguente:
| out | ||
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Tabella 3. Tavola di verità dell’XOR.
Questa funzione è chiamata eXclusive-OR (OR esclusivo). Corrisponde al latino aut, mentre l’OR tradizionale corrisponde al latino vel.
Una possibile notazione matematica è la seguente:
|
| (5) |
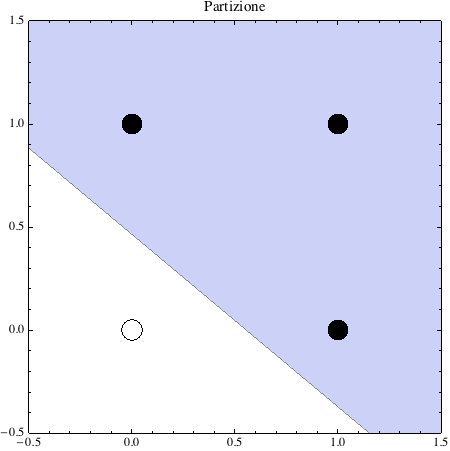
Ecco il grafico degli stati di input della funzione XOR:
![]()
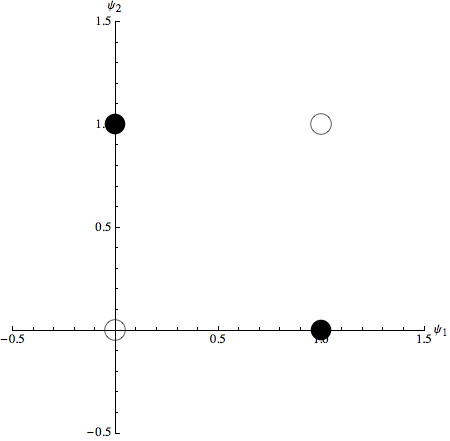
Ora il problema consiste nel tracciare una singola retta che separi gli stati con uscita ‘1’ da quelli con uscita ‘0’.
Naturalmente è facile verificare che non è possibile. Negli anni ‘70 questo problema addirittura provocò il blocco degli studi sulle reti neurali artificiali! Tutto a causa del libro Perceptrons [1] di Minsky e Papert, un attacco alla fattibilità del perceptron. In quel periodo vi erano due paradigmi principali in competizione: il paradigma connessionista o associazionista, rappresentato dalle reti neurali artificiali come il Perceptron, e il paradigma simbolico, una posizione alla Turing sulla manipolazione simbolica sostenuta da Minsky e Papert. [2]
Fortunatamente, l’ostacolo presentato dal problema XOR è di facile soluzione.
Graficamente, abbiamo bisogno di decomporre ulteriormente il problema. Un modo è quello di aggiungere un’altra dimensione al problema, cambiando da un’uscita ‘1’ bi-dimensionale (a due ingressi) ad una tri-dimensionale.
Aggiungiamo quindi la terza dimensione agli stati di input:
Questo ha l’effetto pratico di “sollevare” uno degli input (l’input {1,1}) dal piano dove giaceva insieme agli altri.
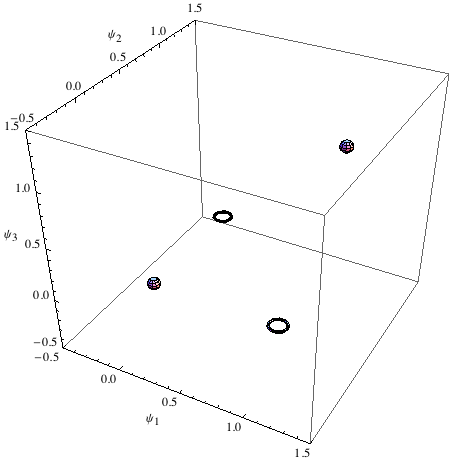
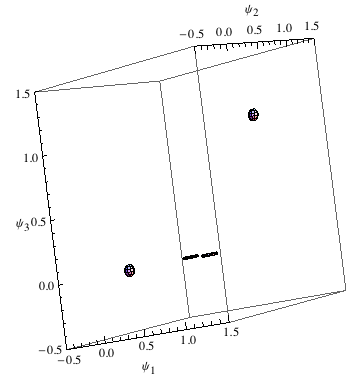
Ecco una visualizzazione della situazione ottenuta mediante un’opportuna modifica della funzione StatePlot[] chiamata StatePlot3D[] (vedi appendice):
![]()
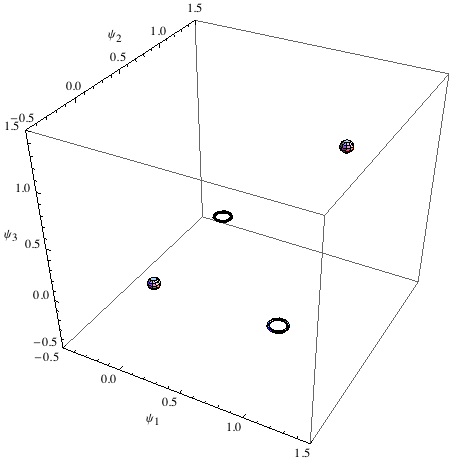
Ora: possiamo creare qualcosa che separerà gli ‘0’ dagli ‘1’? La risposta è sì, faremo uso di un piano invece che di una retta:
![]()
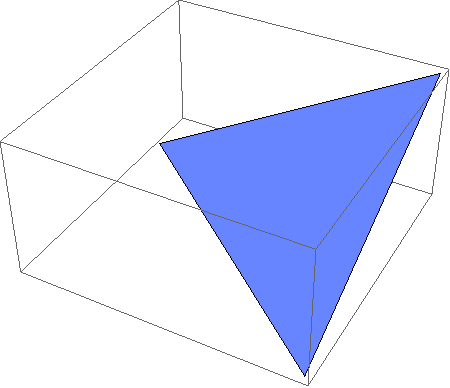
![]()
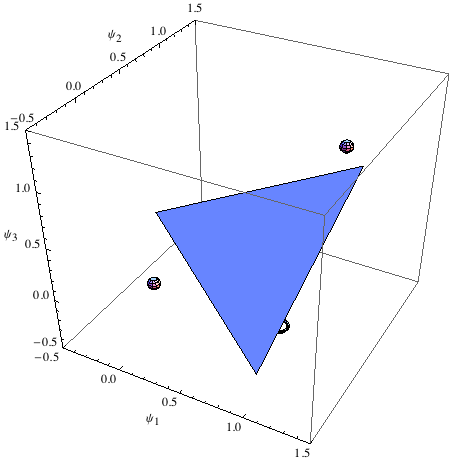
Si noti che il piano che abbiamo introdotto oscura le uscite '0', pur consentendo di vedere gli '1'. Questo è simile alla retta che abbiamo usato per le funzioni AND e OR in precedenza. Ma ora invece di una retta abbiamo un piano che separa le due uscite. Questo piano (così come la retta) è chiamato superficie decisionale o superficie di risposta: vale a dire, separa le due regioni 'risposta'. Se siete su un lato della superficie si produce un tipo di risposta, se siete dall’altra parte se ne produce un altro.
Ricordiamo che l'uscita XOR vale 0 quando entrambi gli ingressi principali sono 0 o 1, e 1 negli altri casi. Nella nostra rappresentazione grafica, i cerchi rappresentano risposte '0' e le sfere rappresentano '1'.
Si scopre che il problema può essere facilmente risolto con l'aggiunta di una semplice modifica:
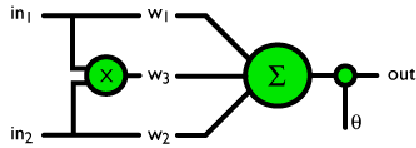
Figura 3. Un neurone artificiale che risolve il problema XOR.
Come si può vedere, abbiamo aggiunto un altro nodo 'speciale', un nodo che moltiplica i due ingressi (Nota: non si tratta solo di una funzione AND?) e che alimenta un altro peso, dopo di che possiamo eseguire l'XOR.
In primo luogo, notiamo che il terzo ingresso nel vettore degli stati è l'AND dei due valori di input. Quindi, possiamo iniziare con i semplici ingressi:
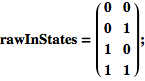
calcolare l'AND di ciascuno mediante la funzione di Mathematica BitAnd[]:
![]()
![]()
e mettere insieme i due vettori:
![]()

In tal modo abbiamo un vettore di input tridimensionale per ciascuno stato, derivato dal vettore bidimensionale originario.
Gli output desiderati per ciascuno degli input sono:
![]()
Ecco un possibile vettore dei pesi:
![]()
Impostiamo anche la soglia:
![]()
Si noti che abbiamo scelto α e θ con attenzione. C'era in realtà una qualche sistematicità in quello che abbiamo fatto, ma non si tratta di una soluzione così semplice ed evidente come l'equazione della retta che abbiamo usato nei casi AND e OR.
Nelle sezioni successive daremo uno sguardo a come possiamo meglio assegnare i pesi in modo più automatico. Per ora, possiamo fidarci del fatto che α e θ sono stati scelti bene.
Abbiamo inoltre creato una funzione Mathematica, Perceptron[], che prende come argomenti una lista di vettori di input, un vettore dei pesi α, e un valore di soglia θ e restituisce una lista di output per gli ingressi dati.
La funzione è definita in appendice, e rende leggermente più efficiente testare una vasta gamma di valori di input.
Possiamo esaminare i risultati per il nostro vettore di stati in questo modo :
![]()
![]()
Avendo in precedenza dichiarato gli output desiderati nel vettore outStates è semplice confrontare gli output ottenuti con quelli teorici:
![]()
![]()
Il risultato conferma che i due output coincidono! La nostra funzione XOR si comporta come richiesto.
References
[1] Minsky, ML, Papert, SA. 1969. Perceptrons: An Introduction to Computational Geometry, MIT Press, Cambridge.
[2] Pollack, JB. 1989. 'No harm intended', Journal of Mathematical Psychology, vol. 33, pp 358–365.
Appendice
Utilità
Disattiva inutili warning
![]()
Funzioni di Plot
Funzione per state plot bidimensionali

Una funzione AND:
![]()
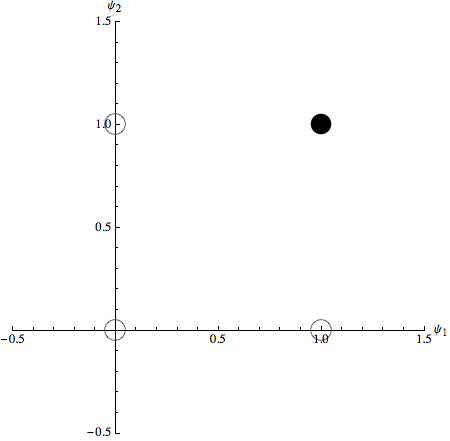
Funzione per plot di stato tridimensionali
![]()

![]()
![]()
![]()
Una Adaline
Presentiamo qui un altro semplice neurone artificiale del tipo Perceptron, chiamato adaptive linear combiner o semplicemente adaline.
![]()
L'implementazione dell'adaline è abbastanza simile al perceptron: occorre ancora moltiplicare gli ingressi per i rispettivi pesi e sommarli (la parte ψ.α), e come funzione di attivazione viene utilizzata la funzione Sign[], che restituisce 1 se il suo ingresso è positivo, 0 se è nullo e -1 se è negativo (è simile alla funzione ![]() discussa in precedenza).
discussa in precedenza).
Graficamente, Sign[] si comporta così:
![]()