Università di Foggia

Dipartimento di Scienze Biomediche

Prof. Crescenzio Gallo

c.gallo@unifg.it

Reti neurali artificiali con Mathematica

Il Neurone

Lezione 1

Introduzione

“Come lavora la nostra mente?” Parecchi autori hanno proposto delle risposte a tale domanda [1,2], forse un po' troppo pretenziose...
Un'altra questione potrebbe essere “Come lavora il cervello?”. Partendo dall'assunzione che il cervello è parte della mente (ma non ne siamo certi [3]) può essere interessante dare un'occhiata a come opera. In [4] è illustrata una panoramica dal punto di vista biologico che, nelle ultime due decadi, è stata completata dall'approccio detto di modellizzazione computazionale (computational modelling), che è quello di cui ci occuperemo.

Modelli

Cos'è esattamente un modello? Una prima definizione potrebbe essere questa: una rappresentazione flessibile di qualche oggetto o sistema 'reale'.

Nel nostro caso, esamineremo modelli che non solo sono flessibili ma che posseggono anche una qualche sorta di potere predittivo — l'abilità di predire un risultato date delle condizioni di input.

Nella pratica vi sono dei cimpromessi da fare nella costruzione di un modello, poiché non è necessario simulare tutte le caratteristiche del sistema originario bensì solo quelle importanti ai fini dello studio del sistema.

Modelli matematici

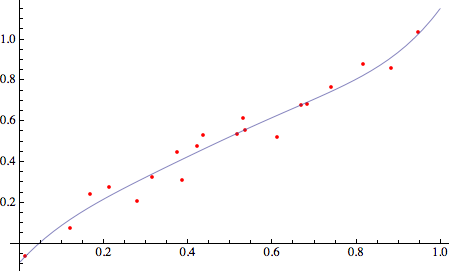
Prendiamo ad esempio la Regressione Lineare. Nella regressione lineare l'obiettivo è quello di “adattare” (fit) una retta rispetto ad una serie di punti in modo da minimizzare l'errore. Al termine del processo di fitting l'equazione della retta può essere utilizzata come una rappresentazione dei dati.

Figura 1. Un esempio di fit lineare.

Nella figura precedente, la retta è descritta dall'equazione y=1.05342x-0.0116236. Questa retta si dice che modella i dati, mediante due parameteri (il coefficiente angolare della retta e l'intercetta), scelti dal processo di regressione per minimizzare l'errore tra i dati reali (i punti rossi) ed il modello (la retta).

Possiamo ora utilizzare questo modello per predire i valori della y per dati valori della x nel modo seguente:

La previsione sembra buona (errore=-0.007). Ma per qualche x vi può essere un errore significativo. Ad esempio:

rispetto invece al valore reale 1.0335, con un errore di 0.044; in questo caso il valore reale di y è sottostimato dal nostro modello che quindi contiene qualche errore. Se si vuole mantenere semplice il modello, dobbiamo convivere con la sua approssimata capacità di previsione. Potremmo naturalmente migliorare (e complicare) il modello utilizzando una curva di regressione non lineare, come nel seguente caso:

con un valore di fit pari a 1.02751 ed un errore (inferiore) di -0.0059852. Naturalmente il modello si complica notevolmente, mentre il beneficio del modello lineare è la sua semplicità.

Modelli cerebrali

Nel nostro studio siamo interessati ad un modello che rappresenti l'operatività funzionale del cervello. In sostanza, a come funziona il cervello: vogliamo quindi costruire un modello funzionale che sia in grado di fare previsioni che possiamo verificare.

Ci sono molti modi di realizzare un modello cerebrale. Per i nostri scopi utilizzeremo il cosiddetto modello riduzionista del cervello (ci sono pro e contro questo tipo di approccio, vedi [6]) con il quale si tenta di capire il quadro generale esaminando i componenti del sistema. Ci accingiamo a modellare le singole unità funzionali che compongono il cervello — un insieme di cellule specializzate chiamate neuroni.

Neuroni

Prima di avviare la creazione di un modello computazionale di sistemi neurali, dovremmo innanzitutto sapere esattamente quello che stiamo cercando di modellare. I sistemi neurali, come il cervello, sono costituiti da cellule specializzate chiamate neuroni.

I neuroni possono essere pensati come sofisticate cellule elettro-chimiche in grado di elaborare informazioni, intendendo con ciò che l'essere in grado di discriminare tra vari stati. Per esempio, possiamo dire se una luce è "accesa" o meno, esaminando il relativo interruttore. Il suo stato (di solito) riflette lo stato della luce (a meno che non sia bruciata la lampadina!).

Stime conservative indicano che il cervello ha più di neuroni, con circa 10.000 varietà. In generale, i neuroni sono costituiti da tre componenti morfologiche principali: i dendriti, il soma e l'assone. Il soma o corpo cellulare è il centro metabolico del neurone, composto dal nucleo della cellula e dai  sistemi di supporto nutrizionale. L ' "output" di un neurone è il suo assone. C'è solo un assone per neurone, ma può variare in lunghezza da circa 10 μm fino ad 1 m! I dendriti agiscono come "input" da altri neuroni. Un neurone "tipico" riceve circa 8-10.000 contatti da altre cellule attraverso i dendriti.
   
Queste connessioni da neurone a neurone sono chiamate sinapsi (in realtà non sono affatto connessioni fisiche, ma piuttosto zone di trasmissione  chimica) sono della forma assone→dendrite dove l'assone (output) di un neurone è collegato al dendrite (input) di un altro.

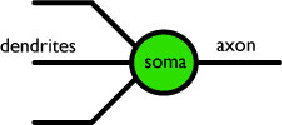
Figura 2. Schema di un neurone. L'informazione scorre da sinistra verso destra. Gli assoni degli altri neuroni si connettono ai dentriti di questo sulle sinapsi. Questo neurone si connette ai dentriti degli altri neuroni mediante il suo assone ed il processo continua, dando luogo ad una rete di neuroni.

Dei 10.000 differenti tipi di neuroni è sufficiente considerare tre categorie generali:

Neuroni Sensoriali
Interneuroni
Neuroni Motorii

I neuroni sensoriali sono responsabili della conversione dell'energia fisica proveniente dall'esterno in informazione neurale, un processo chiamato  trasduzione. Neuroni specializzati nei nostri occhi, sensibili alla luce (chiamati fotorecettori) convertono i fotoni (energia luminosa) in segnali neurali che vengono successivamente elaborati dal cervello. La lingua e il naso hanno neuroni sensibili a varie proprietà chimiche che danno luogo a informazioni sul gusto e l'odorato.
L'informazione ‘entra’ nel neurone come energia meccanica, chimica o luminosa ed  ‘esce’ attraverso l'assone come informazione neurale nella forma di   potenziale di azione.

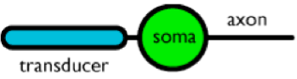
Figura 3. Schema di un neurone sensoriale. L'informazione va da sinistra a destra. Informazione fisica, sotto forma di suono, luce, etc., arriva al trasduttore che converte l'energia fisica in attività neurale. Questo neurone si connette, attraverso le sinapsi dell'assone, ai dentriti degli altri neuroni per convogliare l'informazione attraverso la rete.

I neuroni motorii convertono l'informazione neurale in azione fisica per mezzo dei muscoli. Tutti i muscoli hanno specifici input neurali che dicono loro di contrarsi, estendersi, etc. In queste cellule, il potenziale di azione viene attivato per mezzo di appropriate informazioni ai dentriti ed il potenziale risultante alimenta quindi le fibre muscolari.

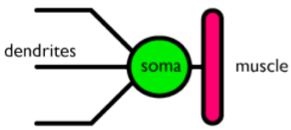
Figura 4. Schema di un neurone motorio. L'informazione va da sinistra a destra. Gli altri neuroni si connettono (attraverso le loro sinapsi) ai dendriti di questo neurone. L'informazione provoca (o inibisce) l'attività fisica del tessuto muscolare connesso.

Tra i neuroni sensoriali e motorii vi è un'ampia raccolta di cosiddetti interneuroni. Questi neuroni si comportano come unità di elaborazione da neurone a neurone — nel nostro corso ci occuperemo principalmente di questo tipo di neuroni.

Gli interneuroni recepiscono l'informazione neurale dagli assoni degli altri neuroni nei loro dentriti. Tali connessioni sono appunto le sinapsi.

Figura 5. Schemat di un interneurone. L'informazione va da sinistra a destra. Gli altri neuroni si connettono attraverso le loro sinapsi ai dentriti di questo neurone, il cui assone a sua volta si connette (per mezzo delle sue sinapsi) con altri neuroni a valle.

Tutti i sistemi neurali sono formati da questi tre tipi di neuroni — neuroni che si specializzano nell'acquisizione di informazioni, neuroni che si specializzano nella trasformazione di informazione neurale in azione, e cellule intermedie che elaborano l'informazione tra i due precedenti tipi di neuroni.

Una macchina comportamentale

Una semplice macchina comportamentale potrebbe essere costruita semplicemente connettendo l'output di un neurone sensoriale all'input di un sensore motorio.

Figura 6. Una semplice macchina di tipo comportamentale. L'informazione fisica viene trasdotta dai neuroni sensoriali. Questi neuroni si connettono direttamente ad un neiurone motorio che decide di attivarsi o no a seconda del suo input. Questa sorta di semplice organizzazione è molto simile alle azioni riflessive negli animali. Ad esempio, supponiamo che i neuroni sensoriali siano trasduttori di calore ed il muscolo sia connesso al braccio. Il calore al punto dei trasduttori fa contrarre direttamente il muscolo, evitando attività cerebrale superiore.

In questo esempio, l'informazione fisica che incide sui trasduttori del neurone sensoriale viene convertita in informazione neurale e trasmessa al neurone motorio, dove un muscolo si contrae.

Portando questa astrazione un po' più avanti, possiamo creare un semplice robot che può essere programmato per manifestare du comportamenti alquanto differenti. Immaginiamo un carrello con quattro ruote, ciascuna delle due ruote frontali controllata da un motore indipendente. I motori funzionano ad una velocità proporzionale alla quantità di informazione neurale ricevuta dai sensori luminosi ad essa connessi.

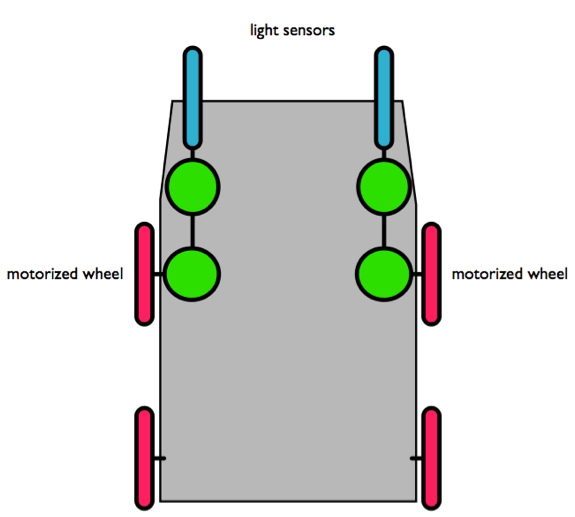
Figura 7. La nostra ‘macchina comportamentale’. Due sensori luminosi sono montati sulla parte frontale e sono connessi a ruote motorizzate. In questa semplice configurazione, ciascun sensore è collegato direttamente al motore retrostante.

Se colleghiamo i sensori come mostrato il carrello diventa un robot ‘cerca luce’. La ruota più vicina ad una sorgente luminosa girerà più rapidamente dell'altra.

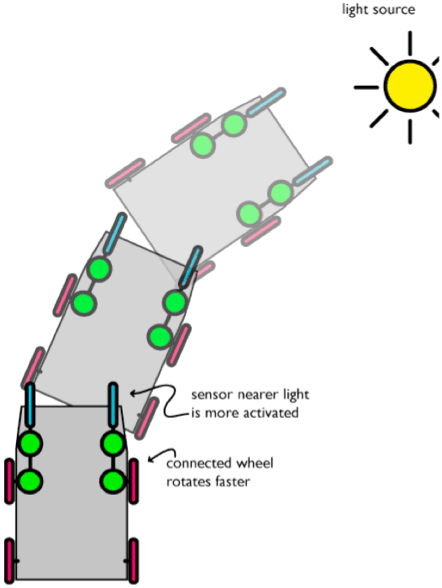
Figura 8. Se esponiamo il nostro robot ad una sorgente luminosa esso si dirigerà verso di essa. Il sensore più vicino alla sorgente luminosa riceverà più luce e quindi farà girare più velocemente il motore ad esso collegato.

Basta però appena ricablare il ‘cervello’ del robot che ne può risultare un comportamento del tutto differente: un robot fotòfobo.

Il robot fotòfobo

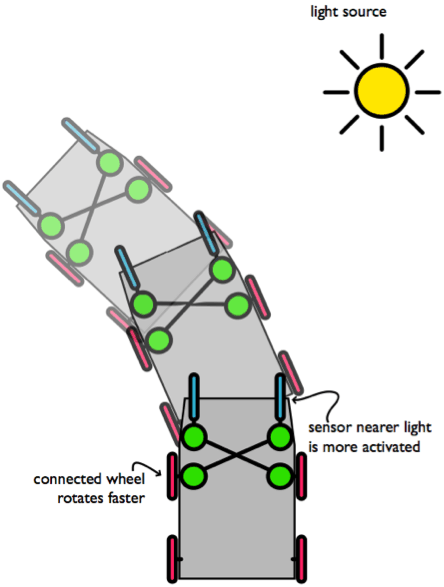
Figure 9. Ua semplice ricablatura del 'cervello' della nostra macchina comportamentale la rende un robot fotòfobo (avverso alla luce). In questo caso, il motore più lontano dalla sorgente luminosa verrà attivato maggiormante. Ciò fa dirigere il robot lontano dalla sorgente luminosa.

Connessioni

Prima abbiamo detto che le sinapsi sono i punti di contatto tra i neuroni. Per essere più specifici, si parla di cellule pre e post-sinaptiche per indicare il neurone a monte e quello a valle della connessione sinaptica con l'assone (output) del primo (pre) che interfaccia i dentriti (input) del secondo (post).

Le connessione sinaptiche tra assoni e dentriti sono essenzialmente di due tipi — eccitatorie (connessioni che inducono l'attivazionedel neurone post-sinaptico) ed inibitorie (che, al contrario, inibiscono l'attivazione del neurone ricevente). In termini di notazione matematica vi sono diversi modi di illustrare tali connessioni. Per i nostri scopi, utilizzeremo un triangolo aperto per indicare le connessioni eccitatorie e triangoli pieni per quelle inibitorie.

Figura 10. Una connessione eccitatoria tra i neuroni A e B. L'informazione va da A→B. Si osservi che in questi diagrammi i dentriti non sono generalmente mostrati; invece, la sinapsi eccitatoria (triangolo aperto) è connessa direttamente al corpo della cellula post-sinaptica. L'attivazione di A incoraggia (ma non necessariamente causa) l'attivazione di B.

Figura 11. Una connessione inibitoria tra i neuroni A e B. L'informazione va da A→B. Si osservi che in questi diagrammi i dentriti non solo generalmente mostrati; invece, la sinapsi inibitoria (triangolo chiuso) è direttamente connessa al corpo della cellula post-sinaptica. L'attivazione di A scoraggia (ma non necessariamente inibisce) l'attivazione di B.

Nel modello del robot proposto prima abbiamo mostrato un sistema nel quale una cellula neurale si connette ad una sola altra cellula. In un sistema più sofisticato, diversi neuroni possono connettersi a molti altri in una varietà di modi.

Tipicamente, un neurone post-sinaptico avrà diversi neuroni pre-sinaptici che vi si collegano ininput. E' l'azione inibitoria ed eccitatoria complessiva che alla fine attiverà o meno la cellula. Si può considerare questo come una sorta di "sistema di voto" in cui ciascun neurone pre-sinaptico esercita una qualche influenza e vince la maggioranza.

Figura 12. Qui le cellule a sinistra convergono verso il neurone a destra (convergenza neurale o fan-in). Una rete completa conterrà molti percorsi convergenti e divergenti.

Questo esempio mostra la convergenza neurale (fan-in) dalle cellule sulla sinistra verso la cellula sulla destra. Diverse cellule ( sono connesse alla cellula B sulla destra. In questo caso particolare e agiscono come inibitori di B, mentre funge da attivatore. In tal modo, in una semplice situazione di "voto a maggioranza", se si attiva e nessuna delle altre due cellule fa altrettanto allora B si attiverà.
Comunque, se o si attivano (cioè inibiscono la trasmissione del segnale) allora l'attivazione di B sarà inibita. Da ciò si deduce che B avrà una connessione inititoria o eccitatorio a valle e le attivazioni di avranno un effetto sulla sua eventuale attivazione.

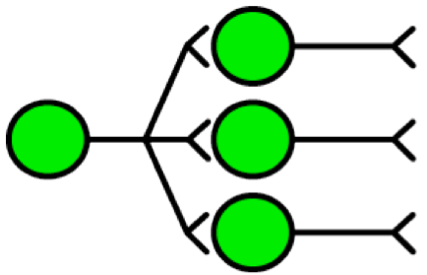
Figura 13. Cellule divergenti. L'assone del neurone a sinistra si ramifica verso diversi altri neuroni. Questa viene chiamata divergenza neurale (o anche fan-out).

Infine, nella figura sopra vediamo un esempio di divergenza (anche chiamata fan-out) della cellula sulla sinistra verso le cellule sulla destra. L'attivazione di un neurone può causare il trasferimento del segnale neurale attraverso l'assone a diversi altri neuroni. Come per la convergenza, le cellule possono connettersi con altre cellule per mezzo di sinapsi inibitorie o eccitatorie, provocando o meno l'attivazione della cellula a valle.

Un tale insieme di connessioni rende possibile eseguire elaborazione di informazioni (cioè calcolo automatico).

Bibliografia

[1]   Pinker, S. 1997, How the Mind Works, WW Norton, New York.

[2]   Fodor, JA. 2000, The Mind Doesn' t Work That Way, MIT Press, Cambridge.

[3]  Hothersall, D. 1995, History of Psychology, McGraw Hill, New York.

[4]   Kandel, ER, Schwartz, JH, and Jessell, TM. 1991, Principles of Neural Science, Elsevier, New York.

[6]   Arbib, MA. 1989, The Metaphorical Brain 2, Wiley, New York.

Created with Wolfram Mathematica 7.0