REQUISITI DI UN ALGORITMO

Un algoritmo è una successione di operazioni applicate a dati (ai quali è attribuito un significato), finito nel tempo, non ambiguo, dettagliato, eseguibile.

D a t i e O p e r a z i o n i

Nella definizione di un algoritmo bisogna:

· definire i dati su cui operare;

· definire le operazioni che devono essere eseguite sui dati.

Dati

Un dato è un “oggetto” al quale si possono attribuire dei valori e sul quale possono essere eseguite operazioni, in relazione al “tipo” del dato.

· numeri interi o reali;

· stringhe di caratteri;

· valori nell’ambito di un insieme qualunque, quali “mesi dell’anno”, “giorni della settimana”, insieme logico contenente i valori “Vero” e “Falso”, etc.

à Un dato è costante se è vincolato ad assumere un solo valore (per esempio Pigreco = 3,14, Giorno festivo = Domenica).

à Un dato non costante è variabile, cioé può assumere qualunque valore dell’insieme di definizione.

Istruzioni

· operative (di calcolo e trasformazione dati);

· di controllo (che controllano la sequenza di operazioni);

· di acquisizione dati (input) e di comunicazioni risultati (output).

Teorema fondamentale dell’Informatica (Boëhm e Jacopini, 1966)

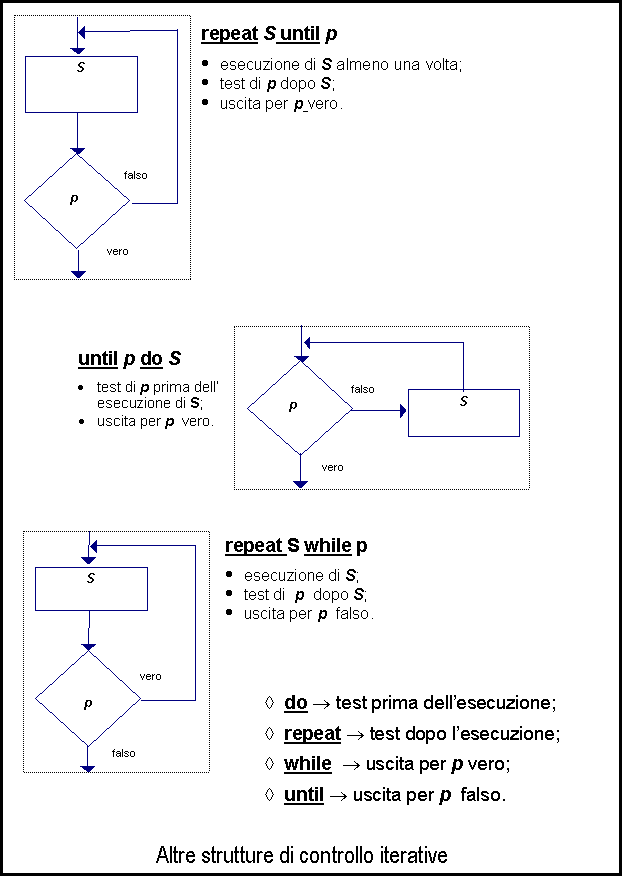
"Con tre sole strutture di controllo si può definire qualunque algoritmo (non concorrente)."

· La sequenza di due (blocchi di) istruzioni S₁ e S₂

· La selezione o alternativa: if p then S₁ else S₂

· L’iterazione o ciclo o loop: while p do S

D a t i S t r u t t u r a t i

· array = dati tutti dello stesso tipo (vettori, matrici, tabelle). Esempio: VET[3]

· record = dati di tipo generalmente diverso. Esempio: ANAGRAFICO.COGNOME

S t r u t t u r e D a t i

Una struttura di dati è una collezione dinamica di dati dello stesso tipo, per i quali non è definita la numerosità.

SEQUENZE:

· file

· coda (First In First Out);

· pila (Last In First Out);

· lista

· insieme

GRAFO

Insieme di elementi detti “nodi”, collegati da “archi” (non orientati) o “frecce” (orientate)

ALBERO

Insieme finito di elementi detti nodi, aventi ciascuno zero, uno o più nodi discendenti ed al massimo un ascendente. I nodi terminali vengono denominati foglie. Esiste un nodo speciale detto radice che non ha ascendenti. I nodi si raggruppano per uguale livello di discendenza, a partire dalla radice che si trova al livello zero. Se in ciascun livello si considera significativo l’ordine con cui compaiono i nodi, l’albero è detto ordinato.

Un albero è binario se ogni nodo ha al max 2 discendenti; può essere effettuata la visita:

· anticipata (radice, sinistra, destra);

· simmetrica (sinistra, radice, destra);

· posticipata o differita (sinistra, destra, radice).

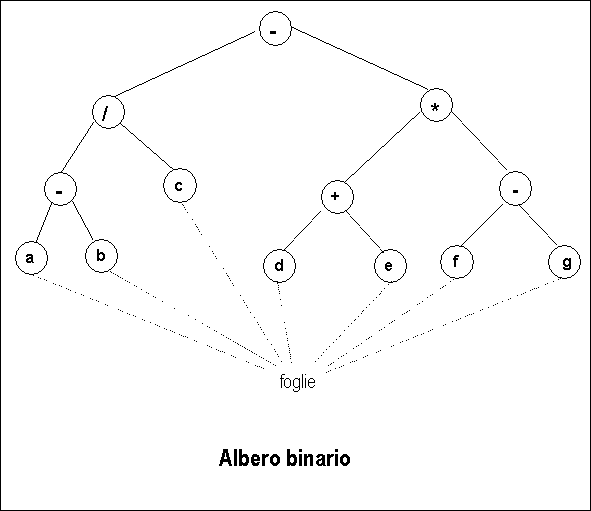
Þ - / - a b c * + d e - f g (visita anticipata)

Þ a - b / c - d + e * f - g (visita simmetrica)

Þ a b - c / d e + f g - * - (visita posticipata)

Visita posticipata ==> NOTAZIONE POLACCA POSTFISSA

EVOLUZIONE DEI LINGUAGGI DI PROGRAMMAZIONE

I generazione (Assembler)

Istruzioni mnemoniche, in corrispondenza 1:1 con quelle macchina.

II generazione (Macro Assembler)

Evoluzione dell’assembler, con “macroistruzioni” (esplose in più istruzioni assembler).

III generazione (Linguaggi Procedurali)

Ad alto livello, indipendenti dal set di istruzioni macchina, di tipo procedurale (imperativo).

IV generazione (Linguaggi Dichiarativi)

Tendono a definire il risultato desiderato mediante “dichiarazioni” (cosa) e non sequenze di operazioni (come).

V generazione (Funzionali/Logici)

Tendono a definire un programma come una relazione funzionale di input/output o un sistema di assiomi (equazioni).